Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами
(18)
Де
Підставивши перший вираз для 
(15) і перший вираз для 
(16) в друге рівняння системи (14) отримаємо рівняння
(19)
Де
Підставивши третій вираз для (15) і перший вираз для (16) в п’яте рівняння системи (14) отримаємо рівняння
(20)
де
Ми отримали систему трьох лінійних рівнянь (18-20) щодо трьох невідомих 
. Розв’язавши її отримаємо
(21)
Із формул (15), (16), (17) і (21) для параметрів 
випливає, що необхідною умовою існування наближення ермітовим сплайном з ланкою (13) є виконання умови 
.
3. Многочленні ермітові сплайни
При 
отримаємо ермітовий сплайн з парною кількістю параметрів 
.
Ланка такого сплайна має вигляд
. (22)
Означення 3. Нехай 
, 
- многочлен 3-го степеня На множині 
задані значення функції 
та її похідної. Кубічним ермітовим сплайном називатимемо функцію з ланкою (22)
, (23)
яка задовольняє систему рівнянь
(24)
де 
- параметри сплайна на 
-й ланці;
Згідно означення 3 параметри ланки ермітового сплайна (23) з ланкою (22) задовольняють системі рівнянь (24)
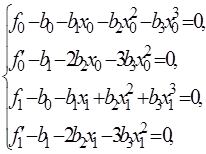(25)
де 
- ліва, а 
- права границі ланки; 
,
. Розв’яжемо систему (25) щодо невідомих 
. Отримаємо формули для обчислень значень параметрів:
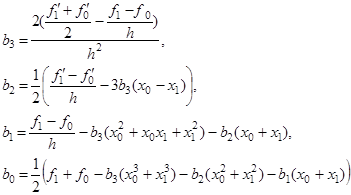(26)
При 
отримаємо ермітовий сплайн з непарною кількістю параметрів 
. Ланка такого сплайна має вигляд
(27)