Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами
Зміст
Вступ
1. Означення ермітових сплайнів з експоненціальними ланками
2. Знаходження аналітичних виразів для параметрів сплайна з експоненціальною ланкою
3. Многочленні ермітові сплайни
4. Похибки наближення ермітовими сплайнами
5. Рівномірне наближення ермітовими сплайнами
Висновок
Список використаної літератури
Додаток
Вступ
Наближення функцій необхідне для практичних розрахунків під час проведення наукових досліджень і в багатьох областях техніки. Аналітично задані функції, які представлені складним виразом, часто необхідно замінити простішим виразом, так, щоб зберігались їх властивості. Це потрібно для обчислення функцій на ЕОМ.
Методи інтерполювання многочленом Лагранжа або Ньютона на відрізку ![]() при використанні великої кількості вузлів інтерполяції часто призводять до поганого наближення, що пояснюється значним накопиченням похибки під час обчислень. Крім того, через розбіжність процесу інтерполяції збільшення кількості вузлів не обов’язково приводить до підвищення точності.
при використанні великої кількості вузлів інтерполяції часто призводять до поганого наближення, що пояснюється значним накопиченням похибки під час обчислень. Крім того, через розбіжність процесу інтерполяції збільшення кількості вузлів не обов’язково приводить до підвищення точності.
Ще одним із способів інтерполювання на відрізку є інтерполювання з використанням сплайн функцій. Сплайн функцією або сплайном називають кусково-поліноміальну функцію, що визначена на відрізку ![]() разом з певним числом неперервних похідних.
разом з певним числом неперервних похідних.
Перевага сплайнів над звичайною інтерполяцію є, по-перше, їх збіжність і, по-друге, стійкість процесу обчислення.
Ряд задач вимагає наближення не тільки самої функції, а й її похідних. Для цього використовують ермітові сплайни. З метою покращення точності наближення функцій сплайнами як ланки можна використовувати не тільки многочлени, а й нелінійні за параметрами вирази.
1.Означення ермітових сплайнів з нелінійним за параметрами виразами в ланках
Наведемо означення ермітових сплайнів з нелінійними за параметрами виразами в ланках (далі нелінійні ермітові сплайни) з парною і непарною кількістю параметрів.
На множині ![]() задані значення функції
задані значення функції ![]() та її похідних до
та її похідних до ![]() - го порядку включно. Потрібно побудувати ермітовий сплайн (тобто вирази для параметрів ланки) з експоненціальною ланкою:
- го порядку включно. Потрібно побудувати ермітовий сплайн (тобто вирази для параметрів ланки) з експоненціальною ланкою:
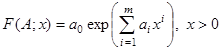 (1)
(1)
де ![]() - параметри ланки сплайна;
- параметри ланки сплайна; ![]() - кількість параметрів
- кількість параметрів ![]() .
.
Означення 1. Нехай ![]() . На множині
. На множині ![]() задані значення функції
задані значення функції ![]() та її похідних до
та її похідних до ![]() - го порядку включно. Нелінійним ермітовим сплайном з парною кількістю параметрів
- го порядку включно. Нелінійним ермітовим сплайном з парною кількістю параметрів ![]() називатимемо функцію
називатимемо функцію
![]() , (2)
, (2)
яка задовольняє систему рівнянь
![]() ,(3)
,(3)
де ![]() - параметри сплайна на
- параметри сплайна на ![]() -й ланці;
-й ланці; ![]() - функція Хевісайда:
- функція Хевісайда:
Із системи (3) випливає, що ![]() . Вираз
. Вираз ![]() називається ланкою ермітового сплайна. Похибка наближення функції
називається ланкою ермітового сплайна. Похибка наближення функції ![]() за допомогою ермітового сплайна
за допомогою ермітового сплайна ![]() характеризується зваженою віддаллю (функцією похибки)
характеризується зваженою віддаллю (функцією похибки)
![]() . (4)
. (4)
Означення 2. Нехай ![]() . На множині
. На множині ![]() задані значення функції
задані значення функції ![]() та її похідних до
та її похідних до ![]() - го порядку включно, а на множині
- го порядку включно, а на множині ![]() задані значення функції
задані значення функції ![]() . Нелінійним ермітовим сплайном з непарною кількістю параметрів
. Нелінійним ермітовим сплайном з непарною кількістю параметрів ![]() називатимемо функцію виду (2), яка задовольняє систему рівнянь:
називатимемо функцію виду (2), яка задовольняє систему рівнянь:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--