Математика / Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами

Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами

(28)

Згідно з означенням 4 параметри ланки (27) ермітового сплайна (23) задовольняють системі рівнянь (28):

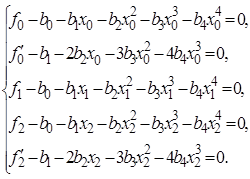(29)

де . Розв’яжемо систему (29) щодо невідомих . Із першого, третього і четвертого рівнянь системи (29) знайдемо вирази для

. (30)

Прирівняємо вирази для (31) із першого і четвертого та першого і третього рівнянь системи (29), отримаємо два вирази для

(31)

(32)

Прирівнявши між собою вирази для із (32) і (33), отримаємо рівняння

(33)

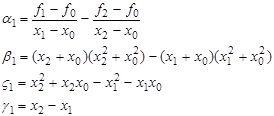
Підставивши перший вираз для (30) і перший вираз для (31) в друге рівняння системи (29) отримаємо рівняння

(34)

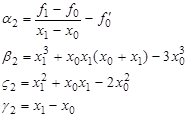
Підставивши третій вираз для (30) і перший вираз для (31) в п’яте рівняння системи (30) отримаємо рівняння

(35)

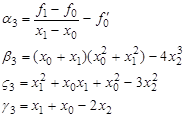
Ми отримали систему трьох лінійних рівнянь (23-35) щодо трьох невідомих . Розв’язавши її отримаємо

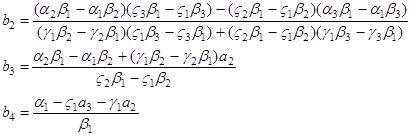(36)

Із формул (30), (31), (32) і (36) для параметрів випливає, що необхідною умовою існування наближення ермітовим сплайном з ланкою (27) є виконання умови .

4. Похибки наближення ермітовими сплайнами

Максимальна похибка рівномірного наближення нелінійними ермітовими сплайнами з парною кількістю параметрів у ланці має вигляд

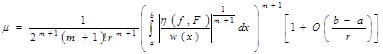, (37)

а для ермітових сплайнів з непарною кількістю параметрів

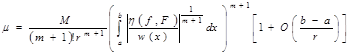(38)

де - кількість ланок сплайна на інтервалі , - вагова функція, - ядро похибки наближення, - дефект ермітового сплайна, . Для ермітового сплайна з ланкою (13) кількість параметрів , дефект сплайна за означенням , величина . Щоб скористатись формулами (37) і(38), потрібно мати вираз для ядра похибки наближення , який би не залежав від параметрів ланки сплайна . Вирази для конкретних ядер можна знайти, використовуючи властивості ядер похибок, які випливають із обмінних теорем.