Курсовая работа: Розвязок інтеграла метоном Нютона Котеса та Сімсона

7 Розробка пакету документів для супроводження комплексу програм

7.1 Інструкція програмісту

7.1.1 Опис вихідного коду

7.1.2 Зміна інтегруючої функції

7.1.3 Зміна тексту допомоги

7.2 Інструкція користувачеві

7.2.1 Запуск

7.2.2 Ввод данних

7.2.3 Перегляд результатів

7.2.4 Вихід з програми

Висновки

Література

Додатки

Додаток А. Технічне завдання

Додаток Б. Лістинг головної програми

Додаток В. Структура дискети

Анотація

Програмний комплекс, що розроблено в даній курсовій роботі створений для знаходження визначеного інтегралу. Програмний комплекс має сучасне багатоієрархічне меню, допомогу. За допомогою даної програми можна виконувати різноманітні визначені інтеграли, від зовсім простих, до досить складних функцій. Результати видаються у вигляді таблиць, що досить зручно, а також можна виводити результати обчислення всіма методами відразу, що дуже зручно при порівнянні методів. Цей комплекс програм розроблений для досить легкого і простого користування.

1 Огляд та варіантний аналіз чисельних методів моделювання

1.1 Основні поняття і визначення

Визначений інтеграл – чисельно рівний площі, обмеженою частиною графіка функції y = f(x), віссю Ох і ординатами f(a) і f(b). Якщо крива перетинає вісь Ох один або декілька разів всередині інтервалу, то інтеграл чисельно рівний алгебраїчній сумі площ, що знаходяться по кожну сторону вісі Ох[6].

Чисельне інтегрування - являє собою стійкий процес і в протиставлення чисельному диференціюванню зменшує дію похибок у початкових даних на кінцевий результат. В основу чисельного інтегрування покладено наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла:

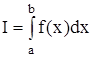
Визначений інтеграл - являє собою площину, обмежену кривою f(x), віссю Х та прямими x=a; x=b[6].

1.2 Класифікація методів рішення поставленої задачі

Інженеру часто приходиться обчислювати визначений інтеграл чисельними методами. Це буває у тих випадках, коли або не вдається виразити інтеграл у замкненій формі, або вона настільки складна, що простіше скористатися чисельним інтегруванням.

Отже основною задачею є обчислення інтегралу виду:

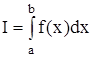
де a і b - нижня та верхня межа інтегрування; f(x) - неперервна функція, відносно якої шукають інтеграл, на відрізку [a,b].

Суть більшості методів обчислення визначених інтегралів заключається в заміні підінтегральної функції f(x) апроксимуючою функцією f(х), для якої можна легко записати первісну в елементарних функціях, тобто

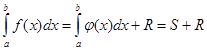
де S - наближене значення інтеграла; R - похибка обчислення інтеграла[2].

Методи чисельного інтегрування, що найбільш часто використовуються на практиці можна згрупувати в залежності від способу апроксимації підінтегральної функції. Дамо коротку характеристику груп найбільш розповсюджених методів.