Курсовая работа: Розвязок інтеграла метоном Нютона Котеса та Сімсона

Сплайнові методи базуються на апроксимації підінтегральної функції сплайнами, що являють собою кусочний поліном. Методи розрізняють по типу вибраних сплайнів. Такі методи є сенс використовувати в задачах, де алгоритми сплайнової апроксимації застосовуються для обробки даних.

В методах найвищої алгебраїчної точності (методи Гаусса-Кристоффеля та інші) використовують не рівновіддалені вузли, розташовані по алгоритму, що забезпечує мінімальну похибку інтегрування для найбільш складних функцій при заданій кількості вузлів. Методи розрізняються способами вибору вузлів і широко використовуються для інтегрування, в тому числі вони можуть бути застосовані і для невласних інтегралів[3].

В методах Монте-Карло вузли вибираються за допомогою датчика випадкових чисел, відповідь носить ймовірний характер. Методи виявляються ефективними при обчисленні великої кратності.

В клас спеціальних групуються методи, алгоритми яких розробляються на основі обліку особливостей конкретних підінтегральних функцій, що дозволяє суттєво скоротити час і зменшити похибку обчислення інтегралів.

1.3 Опис методів моделювання на ЕОМ

Існують такі методи як: метод прямокутників, трапецій, Сімпсона, Ньютона-Котеса, Чебишева, Гаусса. Кожен з цих методів має свої переваги та недоліки. Так наприклад метод прямокутників досить наглядний, простий для розуміння та програмування. Він є так би мовити навчальним методом і необхідний для самого розуміння математичної моделі знаходження визначеного інтегралу. Для інженерних розрахунків знадобляться більш точні методи, наприклад методи Чебишева чи Гаусса[2].

Розглянемо кожний з них більш детально.

1.3.1 Метод прямокутників

Найпростішим методом наближеного обчислення інтеграла є метод прямокутників, геометрична інтерпретація якого зводиться до знаходження визначеного інтегралу як суми площ N прямокутників (з висотою f(x) та основою

отриманих розділень відрізка [а.в] на N рівних частин.(рис.1.1, рис1.2), до того ж якщо розділити на прямокутники зліва на право (див. рис 1.1), то отримаємо формулу лівих прямокутників:

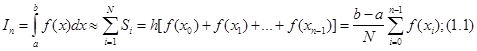
якщо ж розділити на N прямокутників справа наліво (див. рис.1.2), то отримаємо формулу правих прямокутників:

f(x) f(x)

Si

f(Xi)

f(xi)

f(Xn)

Рис.1.1 Рис 1.2

1.3.2 Метод трапецій

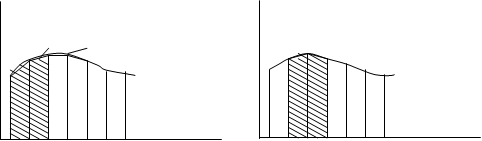
Суть методу трапецій полягає в тому, що інтеграл обчислюється по-іншому, відрізок інтегрування поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюєт ься кусково-лінійною функцією j(х), отриманою стягуванням ординат N відрізків хордами.

f(x)

f(x) j(х)

f(x)

рис.1.3рис1.4

Обчислення визначеного інлдюжегтеграла зводиться до знаходження суми площ Si прямокутних прапецій (рисю1.3, рис.1.4.) N.

Площа кожної такої трапеції (рис.1.4) визначається як

Отже, формула трапеції

Похибка обчислення інтеграла за формулою трапеції оцінюється як