Курсовая работа: Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений

Для построения подобных моделей можно использовать два пути: применять фундаментальные физические соотношения в виде законов сохранения вещества, энергии или восстанавливать параметры моделей по эмпирическим данным, причем второй путь более часто применяется на практике.

2.2 Экспериментальные данные

Для построения математической модели объекта управления использовался метод восстановления параметров модели по эмпирическим данным. Для этого с помощью лабораторной установки были получены экспериментальные данные для исследования объекта управления и построения его математической модели. Результаты снятия экспериментального переходного процесса приведены в Приложении Б. Полученные данные были аппроксимированы в среде научных исследований MatLab. В результате получился график переходного процесса, представленный на рисунке 2.1.

Рисунок 2.1 – Экспериментальный переходный процесс

На рисунке 2.1 по оси ординат отложена температура в °C, а по оси абсцисс – время в секундах. При этом на самом графике кружочками обозначены непосредственно экспериментальные точки, определенные в дискретные моменты времени.

Нормированный переходный процесс представлен на рисунке 2.2.

Рисунок 2.2 – Нормированный переходный процесс

Структура аппроксимирующего выражения для передаточной функции объекта может быть выбрана в общем случае в виде:

Коэффициент усиления объекта управления K_о можно найти по графику переходного процесса. Постоянные времени передаточной функции могут быть найдены методом площадей, геометрическим и методом Ротача.

2.3 Нахождение коэффициента усиления

Коэффициент усиления может быть определен из следующего соотношения:

Отсюда получаем, что .

2.4 Построение математической модели звена первого порядка геометрическим методом

Звено первого порядка с запаздыванием имеет следующий вид:

Для определения величины запаздывания и постоянной времени обратимся к графику переходного процесса (рисунок 2.1). Для нахождения постоянной времени необходимо провести прямую до пересечения с графиком процесса параллельно оси абсцисс на уровне 0.63kc (см.рисунок 2.3).

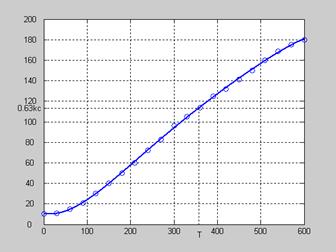
Рисунок 2.3 – Определение постоянной времени по переходному процессу

Постоянная времени T = 360.53 (с). . Построим переходный процесс для такого звена и посмотрим насколько он совпадает с экспериментальным.

Схема модели в MatLab представлена на рисунке 2.4.

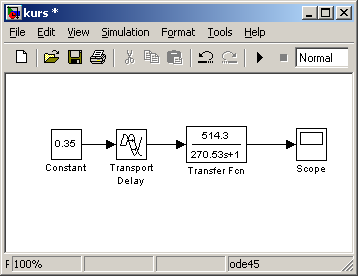
Рисунок 2.4 – Схема модели

Полученный переходный процесс представлен на рисунке 2.5.

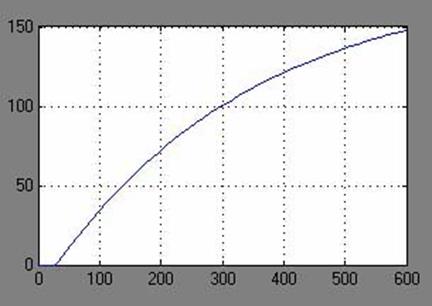
Рисунок 2.5 – Переходный процесс, полученный по передаточной функции

Таким образом, передаточная функция объекта в данном случае имеет следующий вид:

2.5 Построение модели звена второго порядка методом площадей

При q=1 и t=0 получаем объект второго порядка. Рассчитаем постоянные времени T₁ и T₂ при помощи метода площадей: