Курсовая работа: Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений

Рисунок 2.8 – График переходного процесса для звена второго порядка, рассчитанного с помощью метода площадей

2.6 Построение математической модели звена второго порядка методом Ротача

Проведем в точке перегиба касательную, для определения интервала времени Т₀ , заключенного между точками пересечения этой касательной оси абсцисс и линии установившегося значения h_∞ переходной характеристики:

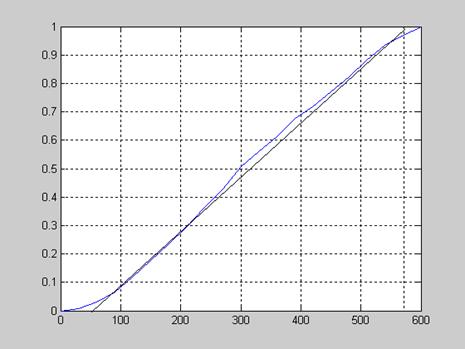
Рисунок 2.9 – Нормированный переходный процесс

Таким образом, запишем величины, являющиеся входными данными:

T₀ =526 tп=90, y(tп)=0,09.

Введем обозначение:

Так как , то возможна аппроксимация инерционным звеном второго порядка без запаздывания (т.е. q=1, t=0), следовательно, получаем следующую модель:

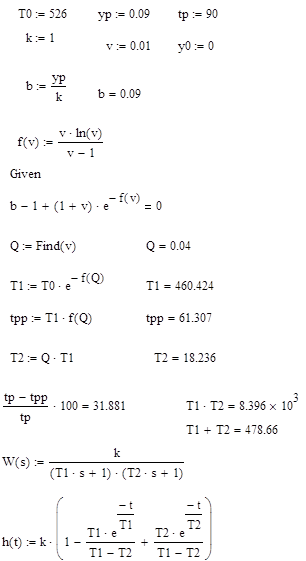
Таким образом, запишем модель звена второго порядка без запаздывания:

или

Теперь построим переходный процесс для данной передаточной функции.

w=tf([514.3],[8396 478.66 1]);

step(w, 600)

grid on

Результат представлен на рисунке 2.10.

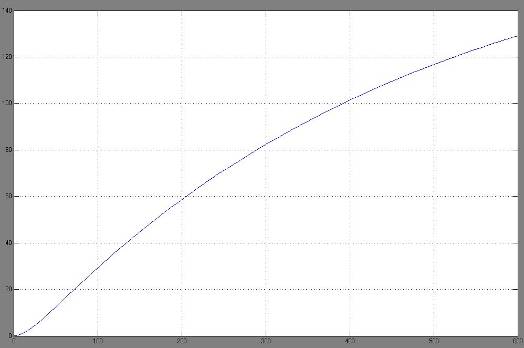
Рисунок 2.10 – График переходного процесса для звена второго порядка, рассчитанного методом Ротача

2.7 Выбор наилучшей аппроксимирующей модели

Для выбора лучшей аппроксимирующей модели объекта управления среди найденных моделей сравним теоретические и экспериментальный переходные процессы. Для оценки качества полученных передаточных функций, описывающих объект управления, вычислим оценку χ² по формуле:

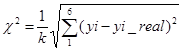
Проведенный расчет дает следующие результаты:

%Расчет погрешностей

k=514.3;

y_real=[24.44 60 93.33 125.5 154.44 180];

y1=[32 72 101 122 136 146];

y2=[31.1 73.3 106.67 131.11 148.89 160];

y3=[30 58.33 63.33 103.33 116.67 128.33];

tmp=0;