Курсовая работа: Система прямого регулювання тиску газу з І-регулятором
DР - відхилення тиску;
m - переміщення регулюючого клапану;
Об'єкт керування: ![]()
¦ - еквівалентне збурення
2. Аналіз і синтез лінійної неперервної САК
2.1 Структурна схема САК
Складаємо структурну схему САК
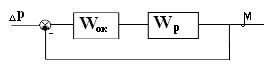
Рис. 1. Структурна схема досліджуваної САК в загальному випадку
Де:
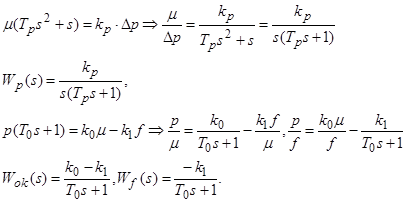
2.2 Визначення передаточної функції розімкнутої та замкнутої САК відносно вхідної
Визначимо передатні функції розімкненої та замкненої САК відносно вхідної:
а) передатну функцію розімкненої САК визначимо як добуток передатних функцій усіх ланцюгів САК, оскільки маємо послідовне з’єднання ланцюгів. Таким чином
w(s)=wок (s)·wр (s) =![]() ,
,
w(s) = ![]() .
.
б) передатну функцію замкненої САК отримаємо за формулою
Ф(s) = ![]() :
:
Ф(s) = ![]() .
.
2.3 Визначення стійкості системи по критерію Гурвіца
Визначимо стійкість системи по критерію Гурвіца:
Знаючи перехідну функцію, знайдемо характеристичне рівняння системи:
D(s)=![]() .
.
На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:
D = 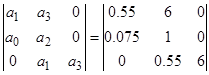 .
.
За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а0 >0 всі визначники Гурвіца були додатними. Умовою стійкості для системи третього порядку будуть: а1 ·a2 >a0 ·a3 .
В даному випадку: а0 = 0,075 > 0; а1 ·a2 = 1,55·1 = 1,55; a0 ·a3 = 0,075·6 =0,45;
1,55>0,45. Умова стійкості системи виконуються, отже за критерієм Гурвіца САК стійка .
2.4 Побудова амплітудно-фазової частотної характеристики (АФЧХ) та визначення стійкості САК за критерієм Найквіста. Дослідження системи методом D – розбиття
Побудова амплітудно-фазової частотної характеристики (АФЧХ) та визначення стійкості САК за критерієм Найквіста. Дослідження системи методом D – розбиття
а). Побудуємо амплітудно-частотну характеристику в визначимо стійкість системи по критерію Найквіста:
1) запишемо перехідну характеристику розімкнутої САК w(s)=![]() .
.
2) в рівнянні перехідної функції проведемо заміну s→j·ω та проведемо всі можливі перетворення та спрощення, тоді
w(j·ω) = ![]() =
=