Курсовая работа: Система прямого регулювання тиску газу з І-регулятором

.

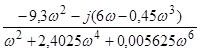Дійсна частина цього виразу

Re(w(j·ω)) = 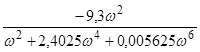= Х(ω),

уявна частина – Im(w(j·ω)) = = У(ω).

3) Побудуємо на комплексній площині (Х0У) криву Найквіста та зробимо висновок про стійкість системи:

У(ω) = 0 → ω = 0 → Х(0) = 0;

У(ω) = 0 → ω = =3,65 →

Х(14) = = -0,273.

По цим точкам побудуємо криву Найквіста (рис. 5).

Критерій Найквіста: Для того щоб замкнута система була стійкою необхідно, щоб годограф розімкненої системи починаючись на дійсній вісі і рухаючись проти годинникової стрілки (при змінній частоті від 0 до ∞) не охоплював точку (-1, j0).

Рис.2. Крива Найквіста.

Замкнена САК охоплює точку (-1, j0), що видно на рис. 5. Отже, САК стійка .

Визначемо запаси стійкості системи:

h=1-0,273=0,727,

j=23°.

б). Дослідження системи методом D – розбиття

За даними, що були отримані в пункті 3.3 знайдемо критичний коефіцієнт підсилення системи k_кр :

1,55 ≥ k·0,075

k ≤ 20,67

k =20,67 (теоретично розрахований коефіцієнт підсилення).

Використовуючи методику D-розбиття та за допомогою програми MathCad побудуємо межу D-розбиття, обравши за параметр дослідження коефіцієнт підсилення системи.

Характеристичний поліном САК, враховуючи, що параметр, який досліджується, коефіцієнт підсилення:

D(p) =.

Звідси k(p) = і k(ωj) =

Побудуємо область D-розбиття, знаючи, що Re(k) = , Im(k) = (див. рис. 6).

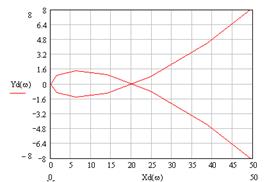
Рис. 3. Область стійкості за параметром k

На побудованій області D- розбиття можна визначити коефіцієнт підсилення (точка перетину області з дійсною віссю).

2.5 Побудова логарифмічної частотної характеристики САК та визначення запасів стійкості