Курсовая работа: Статистика страхования

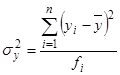, (16)

Соответственно внутригрупповая дисперсия определяется путём суммирования отдельных внутригрупповых дисперсий, взвешенных по частоте.

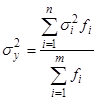, (17)

Для расчёта общей внутригрупповой дисперсии построим вспомогательную таблицу расчёта:

Таблица 2.8 Вспомогательная таблица для расчёта внутригрупповой дисперсии

Группы предприятий по объёму производства, тонн	№ предприятий, входящих в группу	, ед.	, млн. руб.	, млн. руб.	, (млн. руб.)	, (млн. руб.)	, (млн. руб.)
280,6 – 433,2	8	2	1,5	1,195	0,0930	0,093	0,186
	9		0,89		0,0930
433,2 – 585,8	4	2	1,05	1,345	0,087	0,087	0,174
	14		1,64		0,087
585,8 – 738,4	3	2	2,13	2,25	0,014	0,014	0,029
	11		2,37		0,014
738,4 – 891	5	4	2,82	2,788	0,001	0,0299	0,1199
	7		2,73		0,003
	10		3,04		0,064
	12		2,56		0,052
891 – 1043,6	1	6	3,52	3,523	0	0,126	0,753
	2		3,71		0,035
	6		4,1		0,339
	13		3,2		0,104
	15		3		0,274
	16		3,61		0,008
Итого:	16	41,87	1,26
В среднем:	0,079

На основании таблицы 8 определяем:

(млн. руб.)

Для проверки правильности найденных дисперсий воспользуемся правилом сложения дисперсий, согласно которому:

(18)

Подставим найденные значения в формулу (18):

0,866=0,787+0,079 (млн. руб.)

0,866=0,866 (млн. руб.)

Так как правило сложения дисперсий выполняется, то рассчитанные значения дисперсий определены верно.

Определим силу влияния группировочного признака на образование общей вариации, рассчитав эмпирический коэффициент детерминации :

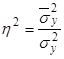, (19)

Получаем: