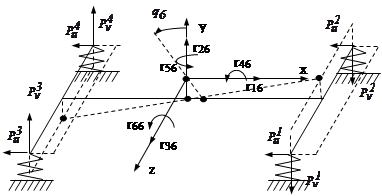
Рисунок 5.7 – Схема нагруженности от q₆

1. Деформации: d_u =U₂ -U₁ =h_c ×q₆ -0=2,044(м); d_v ¹ =d_v ² =V₂ -V₁ =l₁ ×q₆ -0=5(м);

d_v ³ =d_v ⁴ =V₂ -V₁ =l₃ ×q₆ -0=5(м).

2. Силы упругости: P_u =C_u ×d_u =42,95×10⁵ ×2,044=87,777×10⁵ (Н);

P_v =C_v ×d_v =4×10⁶ ×5=2×10⁷ (Н).

3. Реакции:

SX=0; r₁₆ =4×C_u ×h_c =4×42,95×10⁵ ×2,044=351,1×10⁵ (Н);

SY=0; r₂₆ -P_v ¹ -P_v ² +P_v ³ +P_v ⁴ =0; r₂₆ =0 (вагон симметричный);

SZ=0; r₃₆ =0;

SM_x =0; r₄₆ +P_v ¹ ×b₁ -P_v ² ×b₂ -P_v ³ ×b₃ +P_v ⁴ ×b₄ = 0; r₄₆ =0 (вагон симметричный)

SM_y =0; r₅₆ -P_u ¹ ×b₁ +P_u ² ×b₂ -P_u ³ ×b₃ +P_u ⁴ ×b₄ =0; r₅₆ =0 (вагон симметричный);

SM_z =0; r₆₆ -P_u ¹ ×h_c ^* -P_u ² ×h_c ^* -P_u ³ ×h_c ^* -P_u ⁴ ×h_c ^* -P_v ¹ ×l₁ -P_v ² ×l₂ -P_v ³ ×l₃ -P_v ⁴ ×l₄ =0;

r₆₆ =4×87,777×10⁵ ×2,169+4×2×10⁷ ×5=476,1×10⁶ (Н×м).

5.3 Математическая модель виброзащитной системы вагона

На кузов вагона действует система реакций сил упругости, обусловленная колебаниями . Реакции в связях по направлению координатных осей от .суммируются, образуя в узле вектор реактивных усилий:

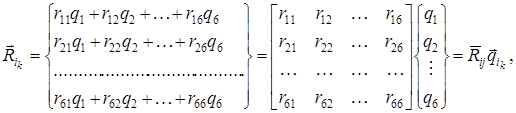(5.12)

где – матрица коэффициентов жесткости несимметричного вагона:

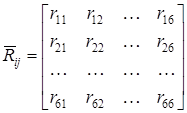,(5.13)

– вектор перемещений центра масс кузова вагона.

6 Внешняя нагруженность динамической системы

6.1 Физическая модель нагруженности вагона

Рисунок 6. 1 - Схема для расчета перемещения колесных пар

Нагруженность характеризуется силами упругости в рессорном подвешивании и реакциями сил упругости в центрах масс тел . Динамическая система получает гармонические возмущения от неровности пути через колесные пары по схеме рисунок 6.1. За начало отсчета принимаем систему координат кузова . Перемещения колес первой тележки по отношению к центру масс кузова имеют опережения, а второй – отставание по фазе, учитываемые углами сдвига фаз :

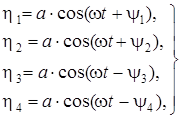,(6.1)

где – углы сдвига фаз в перемещениях колесных пар:

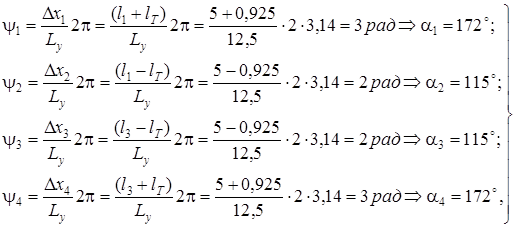,(6.2)

– амплитуда и длина волны вертикальной неровности пути;

– частота вынужденных кинематических возмущений,

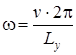(6.3)

При средней скорости движения вагона получим: