Курсовая работа: Структурный, кинематический и силовой анализ механизма. Синтез зубчатой передачи

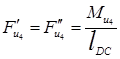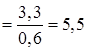; ; (3.8)

Определяем , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:

; (3.9)

Н.

Поскольку составляющую получилась со знаком плюс, то это значит, что ее действительное направление совпадает с выбранным.

Исходя из значений сил, входящих в уравнение равновесия, Н:

; ; ; ;

; ; (3.10)

задаемся масштабом плана сил , Н/мм.

Максимальной силой является сила полезного сопротивления, которую в примере изобразим вектором длиной 250 мм. Получаем масштаб плана сил, Н × мм^-1 :

. (3.11)

Вычисляем длины векторов, мм, изображающих эти силы, поделив их численные значения на масштаб:

; ;

; (3.12)

(задались);

От произвольной точки – полюса плана сил – параллельно силе откладываем вектор изображающий эту силу; от конца вектора параллельно силе откладываем в том же направлении вектор и далее векторы всех сил. Через точку а параллельно звену СDпроводим линию действия , а через конец вектора перпендикулярно к направляющей ползуна – линию действия силы . Точка пересечения этих линий действия определяет силы , , Н:

; (3.13)

;

Далее следует отсоединить группу Ассура АВСО₂ , состоящую из звеньев 2 и 3, вычертить ее в масштабе. В соответствующих точках приложить действующие силы: . Реакцию в шарнире А и О₂ представить в виде двух составляющих – , , , . Реакцию со стороны звена 4 на звено 3 , полученную из плана сил группы Ассура CD, приложить в обратном направлении в точке С звена 2 .

Составляем векторное уравнение равновесия сил, действующих на группу Ассура 2 – 3 , по порядку звеньев:

. (3.17)

Силы ,, и в уравнение не вписываем, так как это уравнение решается построением плана сил, и они взаимно уравновешивают друг друга. Но для определения и эти силы надо знать, определяем их, Н:

(3.1)

;

Из уравнения моментов относительно точки В для звена 2 определяем составляющую , Н:

(3.19)

отсюда,