Курсовая работа: Суммирование расходящихся рядов
![]() (2)
(2)
называется бесконечным рядом , а сами числа (1) - членами ряда. Вместо (2), пользуясь знаком суммы, часто пишут так:
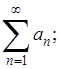 (2а)
(2а)
Станем последовательно складывать члены ряда, составляя (в бесконечном количестве) суммы;
![]() (3)
(3)
их называют частичными суммами ряда.
Конечный или бесконечный предел А частичной суммы ![]() ряда ( 2) при
ряда ( 2) при ![]() :
: ![]()
называют суммой ряда и пишут
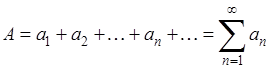 ,
,
Придавая тем самым символу (2) или (2а) числовой смысл. Если ряд имеет конечную сумму, его называют сходящимся, в противном же случае (т. е если сумма равна ![]() , либо же суммы вовсе нет) - расходящимся.
, либо же суммы вовсе нет) - расходящимся.
Примеры.1) простейшим примером бесконечного ряда является уже знакомая геометрическая прогрессия:
![]()
Его частичная сума будет (если ![]() )
)
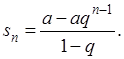
Если знаменатель прогрессии, q, по абсолютной величине меньше единицы, то ![]() имеет конечный предел
имеет конечный предел
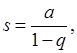
то есть наш ряд сходится, и ![]() будет его суммой.
будет его суммой.
При ![]() та же прогрессия дает пример расходящегося ряда. Если
та же прогрессия дает пример расходящегося ряда. Если ![]() , то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет. Отметим, в частности, любопытный ряд, который получается при a=1 и q= - 1;
, то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет. Отметим, в частности, любопытный ряд, который получается при a=1 и q= - 1;
![]() …
…![]() 1+ (-1) +1+ (-1) +1+…
1+ (-1) +1+ (-1) +1+…
Его частичные суммы попеременно равны то 1, то 0.
2) Легко установить расходимость ряда
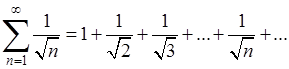
В самом деле, так как члены его убывают, то его n -я частичная сумма
![]()
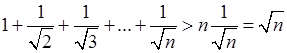
и растет до бесконечности вместе с n.
1.2 Истоки проблемы
Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”.
Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ряды нередко встречались в математической практике.
Хотя применение их при доказательствах и оспаривалось, тем не менее иной раз делались попытки придавать им даже числовой смысл.
Вспомним, опять, наш колеблющийся ряд