Курсовая работа: Суммирование расходящихся рядов
(10)
Если взять любое 
(при 
), то используя предположенное неравенство 
, можно получить такую оценку снизу:
,
откуда, суммируя по m , найдем
.
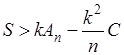Отсюда, сопоставляя с (10), приходим к такому неравенству:
. (11)
Станем теперь произвольно увеличивать п до бесконечности, а изменение k подчиним требованию, чтобы отношение 
стремилось к наперед заданному числу 
. Тогда правая часть неравенства (11) будет стремиться к пределу 
, так что для достаточно больших значений п будет
. (12)
Совершенно аналогично, рассматривая сумму
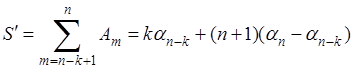
и проведя для 
(при 
) оценку сверху:
,
придем к неравенству
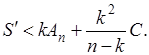
Отсюда
Если 
и одновременно 
, как и прежде (но на этот раз пусть 
), то правая часть этого неравенства стремится к пределу
.
Следовательно, для достаточно больших n окажется
. (13)
Сопоставляя (12) и (13), видим, что, действительно,
.
Теорема доказана.
3.4 Применение обобщенного суммирования к умножению рядов
Остановимся на применении обобщенных методов суммирования в вопросе об умножении рядов по правилу Коши. Пусть, кроме ряда (А ), дан ещё ряд
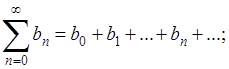(В )
тогда ряд
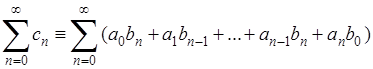(С )