Курсовая работа: Суммирование расходящихся рядов

Имеем при любом натуральном N

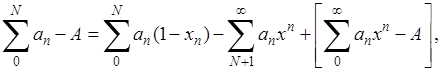
так что:

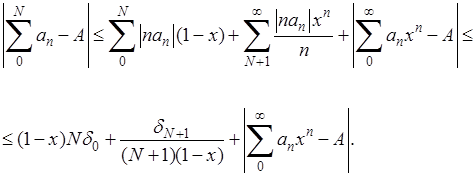
Взяв произвольно малое число , положим

Так что при . Пусть теперь выбрано достаточно большим чтобы: выполнялось неравенство ; соответствующее x было настолько близко к 1, что

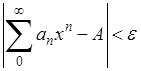. Тогда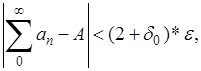

Что и доказывает утверждение теоремы.

К рассмотренному частному случаю теоремы приводится и общий. Положим

так что

и затем

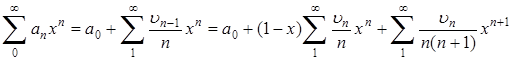(7)

Но из предположения теоремы, т.е. из того, что 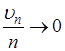при , легко получить, что

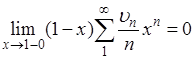. (8)

Для доказательства этого достаточно разбить здесь сумму на две:

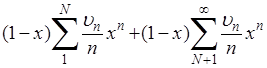
и выбрать N таким, чтобы во второй сумме все множители были по абсолютной величине меньшими наперед заданного числа , тогда и вторая сумма по абсолютной величине будет меньше , каково бы ни было х ; относительно первой суммы, состоящей из определенного конечного числа слагаемых, того же можно достигнуть за счет приближения х к 1.

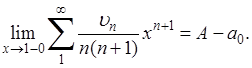
Но здесь уже можно применить доказанный частный случай теоремы, так что и

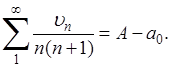С другой стороны,

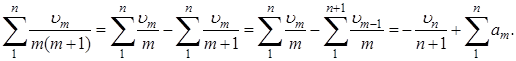
Отсюда, так как первое слагаемое справа стремится к нулю

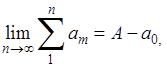
Что и завершает доказательство теоремы.

Глава 3. Метод средних арифметических

3.1 Суть метода

Идея метода в простейшем его осуществлении принадлежит Фробениусу, но связывают его обычно с именем Чезаро, который дал методу дальнейшее развитие.

По частичным суммам данного числового ряда (А) строятся их последовательные средние арифметические

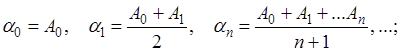
Если варианта при имеет предел А, то это число и называют “обобщенной (в смысле Чезаро) суммой” данного ряда.