Курсовая работа: Суммирование расходящихся рядов

Содержание

Введение

Глава 1. Основные понятия теории рядов

1.1 Определения и термины

1.2 Истоки проблемы

Глава 2. Метод степенных рядов

2.1 Суть метода

2.2 Теорема Абеля

2.3 Теорема Таубера

Глава 3. Метод средних арифметических

3.1 Суть метода

3.2 Взаимоотношение между методами Пуассона-Абеля и Чезаро

3.3 Теорема Харди-Ландау

3.4 Применение обобщенного суммирования к умножению рядов

Глава 4. Другие методы обобщенного суммирования

4.1 Методы Г.Ф. Вороного

4.2 Обобщенные методы Чезаро

4.3 Метод Бореля

4.4 Метод Эйлера

Заключение

Список использованной литературы

Введение

Как мы уже знаем математический анализ, занимается проблемами изучения множества объектов, таких как: числа, переменные, функции, последовательности, ряды и др. При изучении свойств того или иного объекта могут возникать пробелы или “пустоты". Это возникает тогда, когда наука не может объяснить: “Почему происходит так, а не иначе? ”. Такой казус существовал некоторое время и при изучении рядов, а точнее при изучении расходящихся рядов .

При изучении рядов заданному числовому ряду

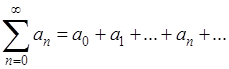(А)

в качестве его суммы мы приписывали предел её частичной суммы , в предположении, что этот предел существует и конечен. “Колеблющийся" расходящийся ряд оказывался лишенным суммы и подобные ряды, как правило, из рассмотрения исключали. Естественно возникает вопрос о возможности суммирования расходящихся рядов в некоем новом смысле, конечно отличном от обычного. Этот вопрос возник ещё до второй половины XIX века. Некоторые методы такого суммирования оказались довольно-таки плодотворными.

В данной своей работе я хочу рассмотреть эти методы, обратить внимание на то, где и какой метод наиболее применим, изучить связь между этими методами. Моя работа состоит из 4 глав, первая из которых содержит основные термины и определения необходимые для работы. Последующие главы рассматривают непосредственно сами методы суммирования. Вторая и третья главы посвящены двум основным методам суммирования: метод степенных рядов и метод средних арифметических , а третья содержит сведения о других существующих, но реже применяемых методах. Каждая из четырех глав содержит примеры суммирования рядов по данному конкретному методу.

Глава 1. Основные понятия теории рядов

1.1 Определения и термины

Как мы упомянули вначале цель нашего исследования - расходящиеся ряды . А что же такое, вообще, ряд ?

Пусть задана некоторая бесконечная последовательность чисел

(1)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--