Курсовая работа: Теоретический анализ модели комплексного числа

Определение 2.1. Суммой комплексных чисел (a,bi) и (c,di) называется комплексное число .

Сумму обозначают знаком «плюс». Поэтому определение можно записать так: .

Так как сложение комплексных чисел сводится к сложению действительных чисел, то сложение комплексных чисел всегда выполнимо и однозначно.

Теорема 2.2. Сложение комплексных чисел коммутативно и ассоциативно.

Доказательство. Проведем для ассоциативного закона. Вычислим . С другой стороны, . Следовательно, .

Комплексное число является нулем, ибо для любого комплексного числа справедливо .

Обычным образом, как, например, для рациональных чисел, доказывается единственность нуля.

Для всякого комплексного числа (a,b) существует противоположное ему комплексное число, обозначаемое . Проверим, что . В самом деле, . Единственность противоположного число доказывается обычным образом.

Теорема 2.3. Вычитание комплексных чисел всегда выполнимо и однозначно.

Доказательство. Проверим, что . Для этого вычислим сумму .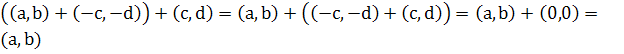

Итак, . Последнее равенство удовлетворяет определению разности, следовательно, . Итак, вычитание выполнимо.

Докажем единственность разности. Пусть есть разность вида . Это значит, что . Прибавим к обеим частям . Получим . Этим доказана однозначность вычитания.

Определение 2.2. Произведением комплексных чисел и называется комплексное число .

Умножение обозначаем точкой, и определение тогда запишем так: .

Так как умножение комплексных чисел сводится к арифметическим действиям с действительными числами, то умножение всегда выполнимо и однозначно.

Теорема 2.4. Умножение комплексных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения, т.е.:

1) ;

2) ;

3) ;

Доказательство. Проверим только дистрибутивный закон. Вычислим левую часть . Вычислим правую часть .

Как видим левая и правая части оказались равными одному и тому же комплексному числу. Следовательно, они равны, т.е.: .

Комплексное число является единицей, ибо для любого комплексного числа справедливо .

Единственность единицы проверяется обычным образом. Пусть есть единица. Тогда , ибо – единица. Но – тоже единица, поэтому . Из однозначности умножения следует, что.

Теорема 2.5. Для всякого комплексного числа существует обратное ему число, обозначаемое , т.е. такое, что их произведение равно единице.

Доказательство. Дано число , где или , т.е. . Найдем такое число , чтобы , откуда . Из определения равенства комплексных чисел следует

Определитель системы , следовательно, система имеет решение, притом единственное: , . Таким образом, .

Следствие. Деление комплексных чисел всегда выполнимо (исключая деление на нуль) и однозначно.

Проверим, что есть . Вычислим: .

Итак, . Последнее равенство удовлетворяет определению частного, следовательно, . Итак, деление выполнимо.