Курсовая работа: Теоретический анализ модели комплексного числа

2) .

Определим однозначное отображение f множества Cʹв С" следующим условием: .

Нетрудно убедиться в том, что f — взаимно-однозначное отображение Сʹна С".

Пусть . Имеем

.

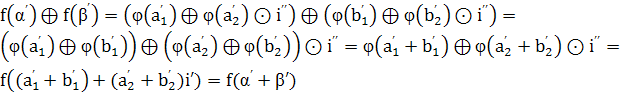Аналогично проверяется и условие .

§5. Непротиворечивость аксиоматической теории комплексных чисел

Теорема 5.1. Аксиоматическая теория комплексных чисел непротиворечива относительно аксиоматической теории действительных чисел.

Доказательство. Мы укажем модель данной теории. Пусть — поле действительных чисел. Рассмотрим множество Р пар действительных чисел и определим на Р бинарные операции Å и 8 (сложение и умножение) следующими условиями:

.

Нам известно, что — поле. Выберем в Р подмножество R0 пар вида (а, 0). Сопоставим с каждым действительным числом а пару . Легко видеть, что φ — взаимно-однозначное отображение Rна R0. Далее, имеем:

.

Таким образом, φ — изоморфное отображение на Следовательно: а) — поле действительных чисел;

б) поле — расширение поля .

Заметим также, что (1, 0) и (0,0) — единица и нуль поля >. Полагаем . Имеем .

Итак, на системе выполняются первые 15 аксиом нашей теории. Пусть, наконец, М — подмножество Р такое, что:

а) ;

б) ;

в) ;

г) .

Докажем, что в таком случае любой элемент множества Р принадлежит множеству М. В самом деле, имеем .

Теорема доказана.

§6. Модели комплексных чисел

Построение моделей систем комплексных чисел способствовало лучшему пониманию их природы.

Пусть М – множество матриц второго порядка над полем действительных чисел вида . Множеству М принадлежит: нулевая матрица 0, единичная матрица Е и матрица I:

.

Проверим, что множество М замкнуто относительно сложения и умножения матриц, т.е. что сумма и произведение матриц принадлежат М:

(1)

Легко проверить, что умножение матриц коммутативно. Так как для матрицы определитель , то существует обратная матрица и, следовательно, в М осуществляется деление. Так что множество матриц из М образует поле.