Курсовая работа: Теория игр 2
, 
, 
, 
.
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi 
, при которых
, 
. 
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, 
, при которых
, 
. 
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi 
, qj 
и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
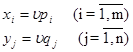
4.1 Решение задач
Пример 5: Найти решение игры, определяемой матрицей.
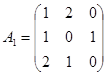
Решение.
Составим теперь пару взаимно-двойственных задач :
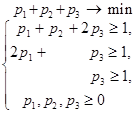
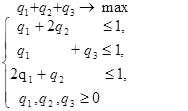
Решим вторую из них
|
Б.п. |
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
Решение |
å |
Отношение |
|
|
-1 |
-1 |
-1 |
К-во Просмотров: 1226
Бесплатно скачать Курсовая работа: Теория игр 2
|
