Курсовая работа: Типовой алгоритм синтеза комбинированной системы автоматического управления

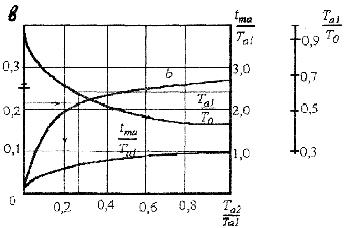
Рис. 3. Номограмма для определения параметров передаточных функций

По номограмме (рис. 3.) можно найти , по известным и . По известному значению находим значение , после чего определяем , и, следовательно:

Подставляя рассчитанные значения в формулу (1.3), получаем вторую математическую модель ОУ:

Третью модель определяем по методу Лукаса:

,

где ;

Таким образом, получили третью математическую модель ОУ:

Далее с помощью программы «СС» на ЭВМ строим переходные процессы полученных функций и наносим их на график с экспериментальной характеристикой (приложение 1).

Вычислим погрешности аппроксимации полученных передаточных функций по интегральному критерию по формуле:

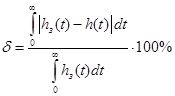
где:

- аппроксимирующая переходная характеристика;

- заданная переходная характеристика.

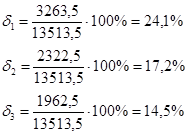
Выбираем передаточную функцию, имеющую наименьшую погрешность аппроксимации:

(1.5)

1.2 Аппроксимация переходной характеристики объекта по возмущающему каналу

Исследуемый объект по возмущающему каналу также является объектом с самовыравниванием (рис. 2.). Поэтому первая аппроксимирующая передаточная функция примет форму оператора (1.1).

Проведём касательную к экспериментальной переходной характеристике в точке перегиба с координатами (t_п ; h(t_п )) (приложение 2.). Определим параметры передаточной функции:

К_об = h_уст = 0,28; t_о = 3,1с; Т_о = 9с; h(t_п ) = 0,06; t_п = 5с

Получили передаточную функцию первой модели для возмущающего канала: