Курсовая работа: Тригонометрические уравнения и неравенства

2. Если коэффициент при переменной величине умножить на , то от этого произойдет лишь перестановка правой и левой групп членов.

3. Если последовательных членов бесконечной прогрессии

например , , , ..., , сделать центральными членами прогрессий с одинаковой разностью, равной :

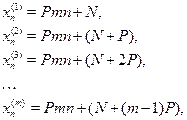
то прогрессия и ряд прогрессий выражают собой одни и те же числа.

Пример Ряд может быть заменен следующими тремя рядами: , , .

4. Если бесконечных прогрессий с одинаковой разностью имеют центральными членами числа, образующие арифметическую прогрессию с разностью , то эти рядов могут быть заменены одной прогрессией с разностью , и с центральным членом, равным любому из центральных членов данных прогрессий, т.е. если

то эти прогрессий объединяются в одну:

Пример , , , обе объединяются в одну группу , так как .

Для преобразования групп, имеющих общие решения, в группы, общих решений не имеющие данные группы разлагают на группы с общим периодом, а затем стремяться объединить получившиеся группы, исключив повторяющиеся.

Разложение на множители

Метод разложения на множетели заключается в следующем: если

то всякое решение уравнения

является решение совокупности уравнений

Обратное утверждение, вообще говоря неверно: не всякое решение совокупности является решением уравнения. Это объясняется тем, что решения отдельных уравнений могут не входить в область определения функции .

Пример Решить уравнение .

Решение. Используя основное тригонометрическое тождество, уравнение представим в виде

Ответ. ; .

Преобразование суммы тригонометрических функций в произведение

Пример Решить уравнение .

Решение. Применим формулу , получим равносильное уравнение

Ответ. .

Пример Решить уравнение .

Решение. В данном случае, прежде чем применять формулы суммы тригонометрических функций, следует использовать формулу приведения . В итоге получим равносильное уравнение