Курсовая работа: Тригонометрические уравнения и неравенства
решениями которого являются значения 
, при которых 
, т. е. числа 
, 
. Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
Если же 
, то эти числа не являются корнями уравнения .
При получим: , 
и левая часть уравнения (1) принимает значение 
.
Итак, при , 
и 
, поэтому можно разделить обе части уравнения на 
. В результате получаем уравнение:
которое, подстановкой 
легко сводится к алгебраическому:
Однородные уравнения с показателем однородности 1. При 
имеем уравнение 
.
Если 
, то это уравнение равносильно уравнению 
, 
, откуда 
, .
Пример Решите уравнение 
.
Решение. Это уравнение однородное первой степени . Разделим обе его части на 
получим: 
, 
, 
, .
Ответ. 
.
Пример При 
получим однородное уравнение вида
Решение.
Если , тогда разделим обе части уравнения на 
, получим уравнение 
, которое подстановкой легко приводится к квадратному: 
. Если 
, то уравнение имеет действительные корни 
, 
. Исходное уравнение будет иметь две группы решений: 
, 
, 
.
Если 
, то уравнение не имеет решений.
Пример Решите уравнение 
.
Решение. Это уравнение однородное второй степени. Разделим обе чести уравнения на , получим: 
. Пусть , тогда 
, 
, 
. 
, 
, ; 
, 
, .
Ответ. 
.
К уравнению вида сводится уравнение
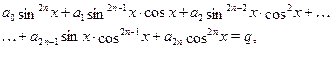
Для этого достаточно воспользоваться тождеством 
В частности, уравнение 
сводится к однородному, если заменить 
на 
, тогда получим равносильное уравнение: 
Пример Решите уравнение 
.
Решение. Преобразуем уравнение к однородному:
