Курсовая работа: Уравнение Дирака в квантовой теории

(1.8)

которое получается эрмитовым сопряжением уравнением (1.5). Как и выше, "" является знаком эрмитова сопряжения, при котором матрицы и транспонируются и комплексно сопрягаются, например

(1.9)

Перестановка с в (1.8) необходима потому, что – строка, и, следовательно, и должны стоять после нее (а не перед ней).

Уравнение неразрывности типа (1.7) можно теперь вывести из уравнений (1.5) и (1.8), если первое умножить на слева, а второе – на справа и сложить получившиеся результаты. Это приводит к уравнению

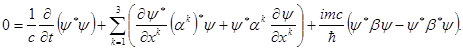(1.10)

Последний член не содержит производных. Поэтому, если мы хотим отождествить уравнение (1.10) с уравнением (1.7), нужно добиться, чтобы этот член был равен нулю. Это можно достигнуть, если потребовать, чтобы

(1.11)

то есть чтобы матрица была эрмитовой. Для отождествления второй группы членов в уравнении (1.10) с дивергенцией мы потребуем далее, чтобы

(1.12)

Другими словами, и и должны быть эрмитовыми матрицами. Другой путь, ведущий к тому же результату,— переписать уравнение (1.5) в гамильтоновой форме:

(1.13)

Ясно, что для эрмитовости H матрицы и должны быть эрмитовыми. Сравнивая (1.7) с (1.10), заключаем

(1.14)

Для вывода дальнейших свойств матриц и нужно исследовать условия, которое накладывает требование, чтобы функция удовлетворяла уравнению

(1.3)

Где

С этой целью умножим уравнение (1.5) на оператор

Который приведет к появлению вторых производных. Члены с и со смешанными пространственно-временными производными сокращаются, и мы получаем

(1.15)

Мы симметризовали здесь член , что можно зделать вследствие коммутации и . Чтобы уравнение (1.15) согласовалось с уравнением Клейна-Гордона, необходимо его правую часть свести к

Это накладывает следующие условия:

(1.16)

(1.17)

(1.18)

то есть матрицы должны антикоммутировать между собой и с матрицей , а квадрат каждой из четырех матриц должен быть равен единице.