Курсовая работа: Уравнение Дирака в квантовой теории

Следовательно,

(3.3)

т. е. вращения представляются ортогональными матрицами. Из (3.3) следует

так что для матриц, удовлетворяющих (3.3), Преобразования, для которых , называют собственными преобразованиями или вращениями, а те, для которых , несобственными ортогональными преобразованиями. Примером несобственного преобразования является отражение в начале координат, которое представляется матрицей

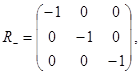(3.4)

причем . Преобразование соответствует переходу от правой системы координат к левой. Каждое несобственное преобразование с может быть записано в виде , т. е. как отражение , вслед за которым уже выполняется вращение; в самом деле,

Совокупность всех вращений в евклидовом трехмерном пространстве образует группу – группу вращений. Группа всех вращений вместе с отражениями называется ортогональной группой. Так как каждый элемент группы может быть охарактеризован заданием трех непрерывно изменяющихся параметров (например, направляющих косинусов оси, вокруг которых совершается вращение, и угла поворота), то группа вращений является непрерывной трехпараметрической группой. Число параметров группы называется размерностью группы.

Вообще представление какой-либо группы G есть отображение (соответствие), сопоставляющее каждому элементу g из G линейный оператор T_g , действующий в некотором векторном пространстве V, и притом такое, что сохраняется таблица умножения для группы, а единица e группы G отображается тождественным преобразованием I в V.

Подпространство V₁ пространства V называют инвариантным подпространством относительно представления T_g , если все векторы в V₁ преобразуются по T_g в векторы , снова принадлежащие V₁ , и это справедливо при всех преобразованиях T_g .

Каждое вращение является вращением вокруг некоторой оси, так что она может быть характеризовано заданием оси вращения, т.е. оси, вокруг которой осуществляется поворот и величины угла поворота. Таким образом, вращение может быть задано вектором , направленным вдоль оси вращения и равным по величине углу поворота. Так, вращение вокруг оси 1 задается вектором , вокруг оси 2 – вектором и т.д. Элемент группы может рассматриваться как функция , т.е. , и тоже относится к представлению: . Вектор соответствует тождественному преобразованию

(3.5)

Рассмотрим бесконечно малые вращения вокруг той или иной оси. Их важность связана с тем, что они порождают однопараметрические подгруппы и что любое конечное вращение может быть построено как последовательность бесконечно малых. Бесконечно малые вращения коммутируют друг с другом, тогда как конечные вращения в общем случае не коммутируют.

Пусть будет матрицей поворота на угол вокруг оси 3, и пусть определена матрица

(3.6)

Оператор называют генератором вращения вокруг оси 3. При бесконечно малом можно записать

(3.7)

Теперь вращения на угол вокруг оси 3 может рассматриваться как результат n поворотов на угол . Поэтому мы можем записать

(3.8)

Аналогичным образом можно определить генераторы вращений вокруг осей 1 и 2. Так как

(3.9)

то явным видом для будет

(3.10а)

и аналогично

(3.10б)

Можно проверить, что генераторы удовлетворяют следующим перестановочным соотношениям:

(3.11)

где – полностью антисимметричный тензор 3-го ранга с компонентами, равными +1, если ljk есть четная перестановка 1 2 3, равными –1, если перестановка нечетная, и равными нулю в остальных случаях. Отметим, что оператор отражения коммутирует со всеми вращениями