Курсовая работа: Уравнение Дирака в квантовой теории

Пусть такая матрица, что . По предположению, , а потом, умножая (2.3) слева и справа на , получаем

(2.4)

где множители возникают в зависимости от того, коммутируют или антикоммутируют и друг с другом. Умножая (2.3) и (2.4) на и вычисляя след, получаем, что . Так как в качестве бралась любая из матриц Г, за исключением единичной, то единственный отличный от нуля коэффициент разложения (2.3) есть , что и требовалось доказать.

Основная теорема о матрицах гласит: если даны две системы матриц и , удовлетворяющих перестановочным соотношениям

(2.5а)

(2.5б)

то существует такая несобственная матрица S, что

(2.6)

Явный вид S дается выражением

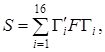(2.7)

где F – произвольная матрица, которая может быть выбрана таким образом, чтобы матрица S была несобственной. Совокупность 16 линейно независимых построена из матриц точно так же, как были построены из . Для доказательства теоремы заметим, что если , где, то тогда , так что . Отметим, что в штрихованной системе число будет тем же самым, т.е , так как его значение определяется только перестановочными соотношениями, а они одинаковы для обеих совокупностей матриц. Так как равно либо , либо , то . Воспользовавшись для S представлением (2.7), получаем

(2.8)

с учетом того, что при фиксированном матрица , находящаяся под знаком суммы по , пробегает все значения 16 элементов алгебры. Это позволило заменить сумму по суммой по . Таким образом, получаем

(2.9)

Так как матрицы неприводимы, то по лемме Шура матрица S является несобственной. Кроме того, с точностью до множителя матрица S определяется однозначно. В самом деле, предположим, что таких матриц S имеется две, скажем и , так что и . Тогда исключая , получаем , т.е. что матрица коммутирует со всеми матрицами и, следовательно, кратен единичной матрице. Отсюда . Часто бывает удобным наложить условие нормировки , которая определяет матрицу S уже с точностью до множителя , равного , или .

Интересен частный случай соотношения (2.7), когда . В этом случае , и S есть матрица, кратная единичной: . Тогда матричный элемент соотношения (2.7) с индексами равен

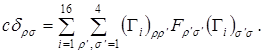(2.10)

Так как это тождество верно при любом выборе матрицы F, то из него следует

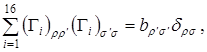(2.11)

где – некоторая постоянная. Для определения этой постоянной свернем индексы и :

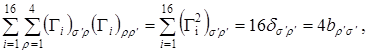(2.12)

откуда , и, таким образом, приходим к тождеству

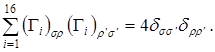(2.13)

3. Спиноры

Связь между координатами точек трехмерного пространства для двух наблюдателей, системы координат которых повернуты друг относительно друга вокруг общего начала, имеет вид

(3.1а)

или

(3.1б)

Длина вектора и угол между векторами остаются неизменными при вращениях, т.е.