Курсовая работа: Уравнение Дирака в квантовой теории
Бесконечно малый поворот вокруг 
на угол 
может быть записан в виде
(3.13)
Соответствующий оператор представления запишем
(3.14)
где 
образуют представление генераторов и удовлетворяют перестановочным соотношениям
(3.15)
Пусть операторы 
. Эти операторы будут эрмитовыми и удовлетворяют перестановочным соотношениям для операторов момента количества движения
(3.16)
В случае группы вращений со всеми генераторами коммутирует оператор 
, и поэтому он является инвариантом группы. Его собственные значения, как известно из теории оператора момента количества движения, равны 
, где 
.Таким образом, каждое неприводимое представление характеризуется положительным целым или полуцелым j, включая 0. Размерность неприводимого представления равна 
при любом весе j, целым или полуцелым. Переходя к классификации неприводимых представлений ортогональной группы, заметим, что линейный оператор 
, соответствующий операции отражения 
, коммутирует со всеми вращениями.
В теории представления групп, осуществляемых комплексными матрицами, фундаментальное значение имеет лемма Шура, в которой доказывается, что необходимое и достаточное условие для неприводимости представления состоит в том, чтобы единственными матрицами, коммутирующими со всеми матрицами представления, были матрицы, кратные единичной.
По лемме Шура в каждом неприводимом представлении он должен быть кратен единичному оператору. Таким образом, неприводимые представления ортогональной группы классифицируются парой индексов 
, где второй индекс является собственным значением , соответствующий данному представлению. При целых j имеем 
(ибо 
), так что существуют два различных неприводимых представления ортогональной группы. В одном из них 
, в другом 
.
При 
представление одномерно, каждый элемент группы отображается единичным элементом, а генераторы тождественно равны нулю. Представление, в котором , назовем скалярным, а то, в котором , – псевдоскалярным.
При 
представление группы вращений двумерно, и генераторы 
могут быть реализованы эрмитовыми матрицами Паули 
, умноженными на 
:
(3.17)
Они удовлетворяют соотношению
(3.18)
Таким образом, в представлении веса оператор поворота на угол 
вокруг оси 3 записывается в виде
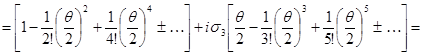
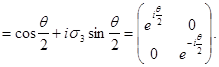(3.19а)
Аналогично, в представлении записываются и операторы поворота на угол вокруг осей 1 и 2:
