Курсовая работа: Вивчення поняття "символ О"

де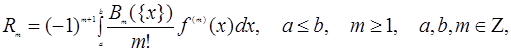

В_k – числа Бернуллі, В_m ({x}) – багаточлен Бернуллі.

В_k = (-1)^k b_2k . [6]

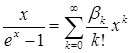. Коефіцієнти b_k обчислюються, використовуючи теорему О одиничність розкладання функції в статечної ряд:

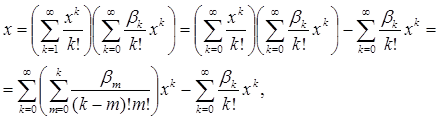
шляхом дорівнюючи коефіцієнтів:

коефіцієнт при х: b₀ = 1,

коефіцієнт при х^k :

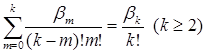
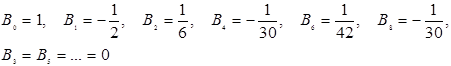
Приклад 1. Знайти .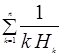

По 1.2.10 Н_k = ln k + O(1). Тоді

.

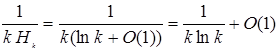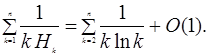
Застосуємо формулу підсумовування Ейлера:

.

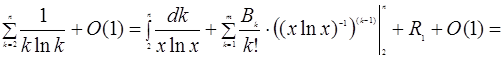
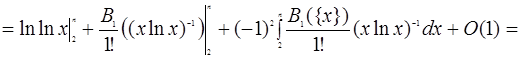
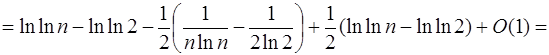
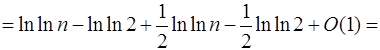
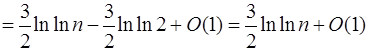Приклад 2. Знайти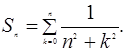

Застосуємо формулу підсумовування Ейлера:

Приклад 3. Знайти асимптотику при n ®¥ суми

Члени цієї суми швидко ростуть із ростом номера, так що головний член асимптотики дорівнює останньому члену суми: S(n) ~ n!, n ®¥. Дійсно,