Курсовая работа: Вивчення поняття "символ О"

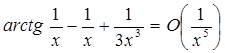. Тоді .

.

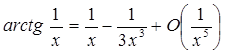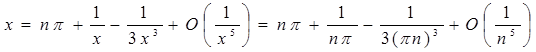І так далі.

2.2Асимптотичне рішення інтегралів

Приклад 1. Обчислити 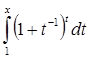при х > 1.

Розкладемо в ряд [6]:

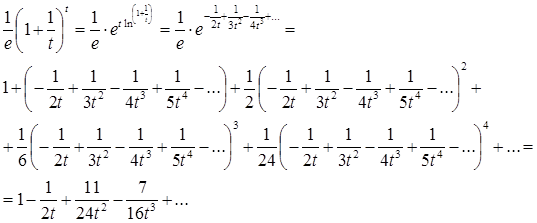
По теоремі (2.1.2)

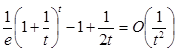, тобто .

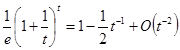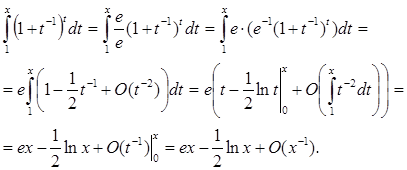
Приклад 2. Обчислити 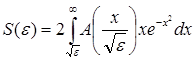при e®+0, , А(х) - східчаста функція: А(х) = 0 при х < 0, А(х) = А_k , k £ x < k + 1, А_k = а₁ + а₂ +…+а_k , а_k = k ^-1 . Причому .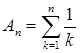

Скористаємося асимптотичною формулою [4]

,

де g - постійна Ейлера 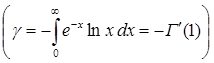. Уведемо функцію Ã(х) = lnx + g.

.

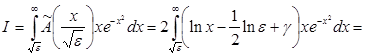
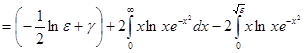Останній інтеграл має порядок О(e ln e) при e®+0, а передостанній – дорівнює -g/2, так що

.

S(e) = I + J, де

.

Оцінимо інтеграл J. Нехай 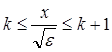, тоді " k ³ 1

.

Ологарифмуємо 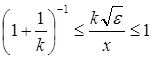, одержимо .

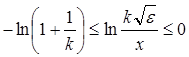Значить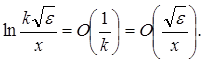

Отже,

.

Одержуємо, що

.

2.3Асимптотичне обчислення суми ряду