Курсовая работа: Вивчення поняття "символ О"

Отже, по визначенню ліва частина є підмножиною правої частини. Співвідношення 5 доведене.

Співвідношення 6: С× O(f(n)) = O(f(n)),якщо З – константа;(1.2.6)

Доказ:

Існує така константа В, що , по визначенню (1.1.1) З = О(1). Тоді З × O(f(n)) = О(1) × O(f(n)) = (по 1.2.4) = O(f(n)).

Співвідношення доведене.

Співвідношення 7: O(f(n)g(n)) = f(n)O(g(n)).(1.2.7)

Доказ:

Покажемо, що ліва частина є підмножиною правої частини.

У лівій частині функції мають вигляд a(n), такі, що існують константи З, n₀ , що

.

По визначенню символу О ми одержуємо вірну рівність (1.2.7). Співвідношення 7 доведене.

Співвідношення 8: O(f(n)²⁾ = O(f(n))² .(1.2.8)

Доказ:

O(f(n)²⁾ = O(f(n) · f(n)) = (по 1.2.7) = f(n) · O(f(n)) = (по 1.2.3) = О(f(n)) · O(f(n)) = O(f(n))²

Співвідношення доведене.

Співвідношення 9: е^(f(n)) = 1 + O(f(n)), якщо f(n) = О(1)(1.2.9)

Доказ:

е^(f(n)) = е^g(n) , де .

Так як. f(n) = О(1), тобто

, те .

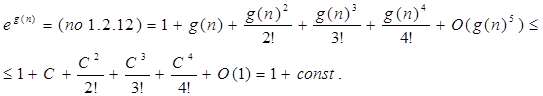
. Значить е^(f(n)) = 1 + O(f(n)).

Співвідношення доведене.

Співвідношення 10: Якщо сума сходиться абсолютно для деякого комплексного числа z = z₀ , те

.

Доказ:

Дане співвідношення очевидно, оскільки

.

Співвідношення доведене.