Курсовая работа: Вивчення поняття "символ О"

= і – 1 + 2(е^-2і+2 + О(е^-4і )) + О(е^-4х) = (по 1.2.6) =

= і – 1 + 2е^-2і+2 + О(е^-4і ) + О(е^-2х × е^-2х) = (по 2.1.1) =

= і – 1 + 2е^-2і+2 + О(е^-4і ) + О(О(е^-2і )× О(е^-2і )) = (по 1.2.4) =

= і – 1 + 2е^-2і+2 + О(е^-4і ) + О(О(е^-4і )) = (по 1.2.5) =

= і – 1 + 2е^-2і+2 + О(е^-4і ) + О(е^-4і ) = і – 1 + 2е^-2і+2 + 2О(е^-4і ) = (по 1.2.6) =

= і – 1 + 2е^-2і+2 + О(е^-4і ).

Таким чином, x = і – 1 + 2е^-2і+2 + О(е^-4і ) - цей четверте асимптотичне наближення кореня.

Продовжуючи цей процес, одержимо послідовність наближень із помилками, асимптотичний порядок яких постійно убуває. Збіжність цієї послідовності при необмеженому зростанні числа кроків на основі проведених міркувань побачити важко, але чисельні можливості цього процесу можна оцінити, взявши, наприклад, і = 5:

1) х = 5;

2) х = і – 1 + О(1) = 5 – 1 = 4; (не враховуємо помилку О(1))

3) x = і – 1 + О(е^-2і ) = 5 – 1 = 4; (не враховуємо помилку О(е^-2і ))

4) x = і – 1 + 2е^-2і+2 + О(е^-4і ) = 5 – 1 + 0,000670925…=4,000670925..... (не враховуємо помилку О(е^-4і ))

Точне значення, отримане стандартними чисельними методами, дорівнює 4,0006698...

Приклад 2.

Знайдемо більших позитивних корінь рівняння

x tg x = 1

Це рівняння можна звернути в такий спосіб:

,

де n – ціле число, а арктангенс приймає значення в інтервалі , знаходимо, що x ~ np при (n → ¥).

Якщо x > 1, то [6]

1). По теоремі (2.1.2)

.

.

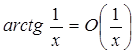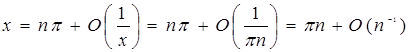2).

По теоремі (2.1.2)

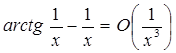. Тоді .

.

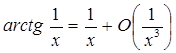3).