Курсовая работа: Вивчення поняття "символ О"

для всіх цілих n. Можна одержати більше точну формулу

_n = О(n² ), тому що

для всіх цілих n. Можна також недбало відкинути частина інформації й записати _n = О(n¹⁰ ).

Визначення О не змушує нас давати найкращу оцінку.

Розглянемо приклад, коли змінна n – не целочисленна.

Приклад 2:

,

де х – речовинне число.

Тут уже не можна сказати, що S(x) = O(x³ ), тому що відношення необмежено росте при х®0. Не можна також сказати, що S(x) = O(x), тому що відношення необмежено росте, коли х прагне до нескінченності. Виходить, ми не можемо використовувати символ "О" для оцінки S(x).

Ця дилема дозволяється завдяки тому, що на змінні, використовувані із О, звичайно накладаються які-небудь обмеження. Якщо, наприклад, ми поставимо умову, що , або що , де e - довільна позитивна константа, або що х – ціле число, то ми зможемо записати S(x) = O(x³ ). Якщо ж накладена умова або , де з – довільна позитивна константа, то в цьому випадку S(x) = O(x). "О велике" залежить від контексту, від обмежень на використовувані змінні.

Ці обмеження часто задаються у вигляді граничних співвідношень.

Визначення 2: співвідношення f(n) = O(g(n)) при n®¥ означає, що існують дві константи С и n₀ , такі, що

при всіх n ³ n₀ .(1.1.3)

Зауваження 1: Значення С и n₀ можуть бути різними для різних О, але вони не залежать від n.

Визначення 3: запис f(х) = O(g(х)) при х®0 означає, що існують дві константи С и e, такі, що

,якщо тільки .(1.1.4)

Тепер О представляє невизначену функцію й одну або дві невизначені константи, що залежать від контексту.

Зауваження 2: запис коректний, але в цій рівності не можна міняти місцями праву й ліву частини. У противному випадку ми можемо прийти до безглуздих висновків, на зразок n = n² , виходячи з вірних тотожностей n = О(n² ) і n² = О(n² ).

Працюючи із символом "О" ми маємо справу з однобічними рівностями. Права частина рівняння містить не більше інформації, чим ліва, і фактично може містити менше інформації; права частина є "огрубінням" лівої.

Якщо говорити строго формально, то запис O(g(n)) позначає не якусь одну функцію f(n), а відразу множина функцій f(n), таких, що для деякої константи С. Звичайна формула g(n), що не включає символ О, позначає множину, що містить одну функцію f(n) = g(n). Якщо S і T суть множини функцій від n, то запис S + T позначає множину всіх функцій виду f(n) + g(n), де f(n)ÎS і g(n)ÎT; інші позначення начебто S – T, ST, S/T, , е, ln S визначаються аналогічно. Тоді "рівність" між двома такими множинами функцій є теоретико-множинне включення; знак "=" у дійсності означає "(".

Приклад 3: "Рівняння" означає, що S₁ Í S₂ , де S₁ є множину всіх функцій виду , для яких найдеться константа З₁ , така, що , а S₂ є множина всіх функцій , для яких найдеться константа З₂ , така, що .

Можна строго довести це "рівність", якщо взяти довільний елемент із лівої частини й показати, що він належить правій частині: нехай таке, що , варто довести, що існує така константа З₂ , що 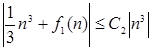. Константа вирішує проблему, тому що для всіх цілих n.

Зауваження 3: Якщо у формулі використовується трохи змінних, то символ О представляє множину функцій від двох або більше змінних, а не тільки від однієї. В область визначення кожної функції входять всі змінні, які в даному контексті "вільні" для зміни.

Отут є деяка тонкість через те, що змінні можуть мати сенс лише в частині вираження, якщо вони зв'язані знайомий ( або подібним.

Приклад 4:

,

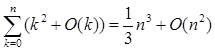ціле n ³ 0.(1.1.5)

Вираження k² + O(k) у лівій частині відповідає множині всіх функцій від двох змінних виду k² + f(k, n), для яких найдеться константа З, така, що для 0 £ k £ n. Сума таких множин функцій для 0 £ k £ n є множину всіх функцій g(n) виду