Курсовая работа: Вивчення поняття відносин залежності

X — базис в A;

X — максимальна незалежна підмножина в A;

X — мінімальна множина, що породжує, в A.

Тоді й .

Доказ:

(i) (ii) Якщо X – базис, то по визначенню 6 X – незалежна підмножина, що породжує. Доведемо від противного, що воно максимальне. Нехай існують незалежні множини . Візьмемо , тоді незалежно, тому що будь-яка підмножина незалежної множини незалежно. Тому по визначеннях 3 і 5 , звідки , одержали протиріччя з умовою. Тому X є максимальною незалежною підмножиною в A .

(ii) (i) Доведемо від противного, нехай не базис в , тобто . Тоді таке, що незалежно й лежить в , одержали протиріччя з максимальністю .

(ii) (iii) Якщо X — максимальна незалежна множина в A , те всякий елемент в A або належить X, або такий, що залежно, а тому в тім і іншому випадку, тобто Оскільки , те X - множина, що породжує. Виходить, - базис простору .

Доведемо тепер, що воно мінімально. Нехай множина . Доведемо, що воно не є породжує для A . Візьмемо , але . Тоді незалежно, як підмножина множини X . Тому по визначеннях 3 і 5 і , а це значить, що Y не є множиною, що породжує. Висновок: X – мінімальна множина, що породжує, в A.

(i) (iii) Справедливо , по доведеним вище твердженнях (i) (ii) і (ii) (iii). :

Визначення - позначення 10.

Для довільної множини простору залежності Z позначимо множину всіх максимальних незалежних підмножин, а через - множину всіх мінімальних підмножин, що породжують, цієї множини.

З теореми 1 випливає, що збігається із множиною всіляких базисів простору й для кожного .

Наступний приклад показує, що зворотне включення вірно не завжди.

Приклад 10.

Розглянемо дев'яти елементну множину , що записана у вигляді матриці 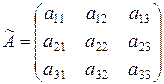. Залежними будемо вважати підмножини множини , що містять «прямі лінії»: стовпці, рядки або діагоналі матриці .

Розглянемо множини й , вони буде максимальними незалежними, тому що не містять прямих і при додаванні будь-якого елемента з , що не лежить у них, стають залежними. Тут максимальні незалежні множини містять різна кількість елементів.

Розглянемо ще одну множину , вона є мінімальним що породжує, тому що якщо виключити з нього хоча б один елемент, то воно вже не буде множиною, що породжує. Легко помітити, що залежно, тому не є базисом. Даний приклад ілюструє, що (iii) (i) не вірно в загальному випадку, тобто для довільних просторів залежності.

Для будь-якого простору залежності Z виконуються наступні властивості:

Заміщення. Якщо

Доказ:

Нехай , . Тому що залежить від , те залежить від незалежної підмножини множини , тобто залежно. Тепер, якби , те було б підмножиною множини й тому , що суперечило б нашому припущенню. Тому . Візьмемо . Тоді незалежно, тому що . Але залежно. Звідки .

Вкладеність. Об'єднання будь-якої системи вкладених друг у друга незалежних множин є незалежною множиною, тобто - незалежно, де також незалежні й

Доказ:

Доведемо від противного. Припустимо, що залежно, тоді в ньому найдеться кінцева залежна підмножина : . Маємо , одержали протиріччя з незалежністю .

Максимальність. Будь-яка незалежна множина втримується в максимальній незалежній множині.

Доказ:

Нехай - довільна незалежна множина в. Утворимо множину Z : всіх незалежних множин, що містять . Відносно множина є впорядкованою множиною, що задовольняє по властивості вкладеності, умові леми Цорна. Тоді по лемі Цорна в існує максимальний елемент .

Теорема 2.