Курсовая работа: Визначення деформації балок при згині

Мал. 8.7

Опорні реакції балки рівні

Згинальні моменти на ділянках / і // виражаються різними формулами, тому треба взяти два довільних перетини х₁ і х₂ і написати два диференціальних рівняння (розглядаємо ліві частини балки)

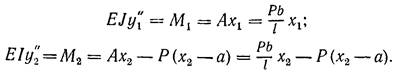(28) (29)

Інтегруючи ці рівняння, одержуємо:

перша ділянка

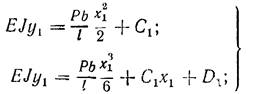(3о)

друга ділянка

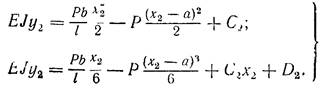(31)

У вираження для у і q увійшли чотири постійних інтегрування, удвічі більше, ніж число ділянок. Для їхнього визначення необхідно мати 4 граничні умови, де що-небудь відомо про прогини і кути повороту. Такими перетинами будуть опорні перетини А і В і перетин С — перетину розділу між ділянками І і ІІ .

Значення у і q у перетині С можна обчислити з формул як для першої ділянки, так і для другої, тобто при х₁ = х₂ = d повинний бути у1 = у2 і q ₁ = q ₂ Таким чином, одержимо дві умови:

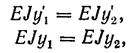(32) (33)

тобто точка розділу завжди дає нам дві умови. Дві інших умови одержимо на опорах

у перетині А при х₁ = 0 прогин у₁ = 0; (34)

у перетині В при х₂ = l прогин у₂ = 0. (35)

Підставляючи перші рівняння виражень (30) і (31) в умову (32) при умові х₁ = х₂ = а, одержуємо

С₁ = С₂ . (36)

Аналогічно з умови (33) з обліком других рівнянь (30) і (31) при х₁ = х₂ = а, одержимо

D₁ = D₂ (37)

тобто постійні інтегрування для обох ділянок виявилися однаковими завдяки прийнятому методу складання й інтегрування диференціальних рівнянь.

Застосовуючи умову (34) до другого рівняння (30), одержимо D₁ = 0, а отже, і D₂ = 0. Застосовуючи ті ж рівняння (35) до другого рівняння (31), одержимо

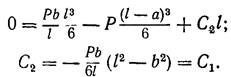(38)

Тепер формули (30) і (31) для y і q запишуться так;

перша ділянка

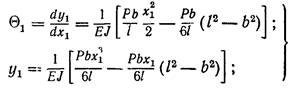(39)

друга ділянка

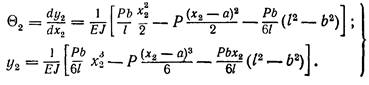(40)