Лабораторная работа: ЭВМ с использованием математического пакета MathCad в среде Windows 98 для использования матричной алгебры в расчетах электротехнических систем


Вычисление собственного вектора для матрицы А и λ3.

Как мы видим, в этом случае собственные вектора и матрица собственных векторов матрицы А, имеют численные значения, отличающиеся знаками. Однако это не меняет общности поставленной задачи, так как речь идёт о пространстве, в котором находятся собственные вектора матрицы А.
2.4.3 Приведение заданной матрицы к диагональному виду
В Mathcad легко создать матрицы определенного вида с помощью одной из встроенных функций, например:
· diag(v) — создаст диагональную матрицу, на диагонали которой находятся элементы вектора v;
Рассмотрим вектор, элементами которого являются собственные значения матрицы А.


![]()

Для квадратной матрицы А часто бывает необходимо найти, если это возможно, такую квадратную матрицу, чтобы выполнялось условие:
Р-1 · А·Р = L
Здесь L представляет собой квадратную матрицу diag (λ1 , λ2 ……. λn ) , где λ1 , λ2 …… λn являются собственными значениями матрицы А.
Найденная выше матрица Р содержит нормированные собственные векторы, соответствующие собственным значениям матрицы А; n-й столбец вычисляемой матрицы соответствует собственному вектору n-го собственного значения.
![]()
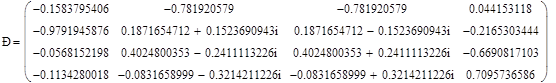
Матрица векторов собственных значений матрицы А приводит ее к треугольному виду:
![]()
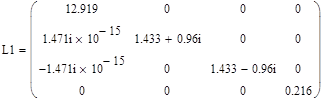
![]()
3. Выводы по работе
В результате выполнения практической работы №1 были изучены возможности математического пакета MathCad в среде Windowsс целью дальнейшего использования матричной алгебры в инженерных расчетах электротехнических систем. Были изучены и повторены основные моменты теории матриц. Изучены способы задания векторов и матриц в среде MathCad. Я научился работать с массивами, векторами и матрицами, применял векторные и матричные операторы и функции. Вторая по частоте применения задача вычислительной линейной алгебры — это задача поиска собственных векторов и собственных значений матрицы. Для решения таких задач в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы. Применение матричных функций намного облегчает расчёты по теоретическим основам электротехники, теории автоматического управления и другим дисциплинам. Как оказалось, особенно просто в MathCad работать с комплексными числами и полиномами высших порядков. Решение характеристических уравнений выдаётся в виде векторов, которые можно далее преобразовывать с помощью матричной алгебры, представленной в MathCad.