Лабораторная работа: Класична лінійна регресія

Розрахункове значення порівнюється з табличним F_таб при n-m i m-1ступенях свободи та вибраному рівні довіри a. Якщо F³F_таб , нульова гіпотеза відхиляється і істотність моделі підтверджується, в протилежному випадку – відхиляється.

17. Гіпотезу про значущість кожного з параметрів b_j економетрічної моделі можна виконати за допомогою t-крітерію. Нульова гіпотеза: b_j несуттєво відрізняються від 0, тобто H₀ : b_j = 0. Розрахункове значення t-критерію:

де c_jj – діагональний елемент j-ї строки (стовпця) матриці ,

- стандартна помилка оцінки j-го параметра моделі.

Якщо t³t_таб , нульова гіпотеза відхиляється і відповідний коефіцієнт регресії є достовірним.

18. На основі t-критерію і стандартної помилки будуються граничні інтервали для оцінок параметрів моделі:

де t_a - табличне значення t-статистики з рівнем довіри a та ступенями свободи n-m.

ПРИКЛАД ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

Нехай маємо змінні:

- середньомісячна зарплата, ум. од.;

- продуктивність праці, ум. од.;

- фондомісткість продукції ум. од;

- виконання норми виробітку,%

Гіпотеза, що пропонується для перевірки - середньомісячна зарплата лінійно залежить від продуктивності праці, фондомісткості продукції та виконання норми виробітку.

Позначимо Y - середньомісячна зарплата, X₁ - продуктивність праці, X₂ - фондомісткість продукції, X₃ - виконання норми виробітку/

Вихідні дані наведено в таблиці.

номер цеху	середньомісячна з/п,Y	Продуктивність праці, X1	ФондомісткістьX2	Норма виробітку, X3
1	45	265	0,2	130
2	42	236	0,04	127
3	50	257	0,3	151
4	55	279	0,2	149
5	40	226	0,1	140
6	70	350	0,1	141
7	56	278	0,25	152
8	57	262	0,03	188
9	55	269	0,15	120
10	53	250	0,32	126

Матриця Х доповнюється стовбцем одиниць для врахування коефіцієнта регресії b₀ :

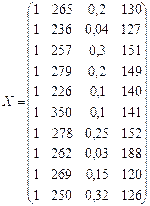
1. Оцінимо параметри регресії за допомогою 1МНК.

Підготуємо необхідні проміжні матриці:

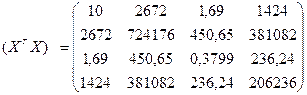
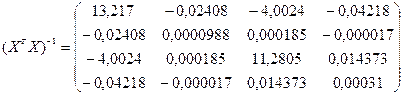
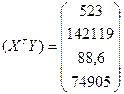
Використовуючи оператор оцінювання МНК, отримуємо

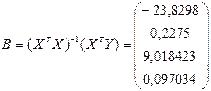
Þ Рівняння регресії має вигляд:

Y = -23,83+0,23X₁ +9,018X₂ +0,097X₃

Ця модель має бути проаналізована на значущість в цілому (2), а також на значущість кожного коефіцієнта регресії зокрема (3).