Лабораторная работа: Класична лінійна регресія
n – кількість спостережень, n=10
m – кількість оцінюваних параметрів моделі, m=4.
Стандартне відхилення залишків ![]() = 4,912352.
= 4,912352.
Отримуємо:
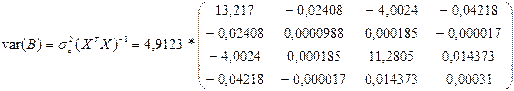 =
=
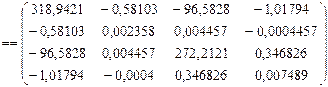
На діагоналі коваріаційної матриці отримуємо дисперсії коефіцієнтів регресії bj :
D(b0 ) = 318,9421,
D(b1 )=0,002358,
D(b2 )=272,2121,
D(b3 )=0,007489
Визначимо значення стандартних помилок коефіцієнтів регресії Sbj :
![]()
Sb0 = ![]() = 17,85895,
= 17,85895,
Sb1 =![]() = 0,048839,
= 0,048839,
Sb2 =![]() = 16,49885,
= 16,49885,
Sb3 =![]() = 0,086537
= 0,086537
| 17,85895 |
| 0,048839 |
| 16,49885 |
| 0,086537 |
Sb =
Розрахункове значення t-статистики отримуємо для кожного коефіцієнта:
tb0 = b0 / Sb0 = -23,83/ 17,85895 = -1,33433 і т. п.
| -1,33433 |
| 4,658181 |
| 0,546609 |
| 1,121298 |
tp =
Розрахункові значення t-статистики порівнюються за абсолютною величиною з табличним t10-4 = 1,943. Параметр вважається статистично значимим (нульова гіпотеза не підтверджується), якщо ![]()
Це означає, що в нашому випадку тільки b1 є статистично значущим і суттєво впливає на модель.
Довірчі інтервали для оцінок регресії будуються за формулою:
b0 =-23,8298±34,699 |
| b1 =0,2275±0,0949 |
| b2 =9,018423±32,0573 |
| b3 =0,097034±0,1681 |
![]() :
:
4. Якість побудованої моделі можна визначити за допомогою коефіцієнта детермінації:
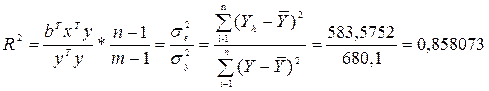 ,
,
Його значення показує, що на 85,8073% варіацію змінної Yможна пояснити варіацією пояснювальних змінних Х.