Лабораторная работа: Класична лінійна регресія
- коефіцієнта множинної кореляції R (визначається як корінь з коефіцієнта детермінації) – показує тісноту зв’язку між Y і всією множиною пояснювальних зміннихX (1 на модель) ;
- парних коефіцієнтів кореляції r, що знаходяться в кореляційній матриці r* і характеризують тісноту зв’язку між Y та окремим Xj .Вони діляться на два типи:
а) парні коефіцієнти кореляції між Y та окремим Xj
б) парні коефіцієнти кореляції між окремими Xk і Xj rXkXj (їх для моделі існує m*m);
- частинних коефіцієнтів кореляції, що також характеризують тісноту зв’язку між Y та окремим Xj , але при умові, що інші незалежні змінні сталі, тобто їх варіація не впливає на залежність між Y та Х:
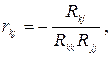
де Rkj – алгебраїчне доповнення до (j,k)-го елемента кореляційної матриці r;
Rkk та Rjj – відповідні діагональні елементи цієї матриці.
За вимогами роботи треба розрахувати коефіцієнт множинної кореляції R:
R = ![]()
де R2 – коефіцієнт детермінації;
![]() 0,926322 – тіснота зв’язку між Y і X для нашої регресії є досить великою.
0,926322 – тіснота зв’язку між Y і X для нашої регресії є досить великою.
Його значущість перевіряється також за допомогою t-статистики (нульова гіпотеза – R незначущо відрізняється від 0). В цьому випадку розрахункове значення крітерію визначається за формулою:
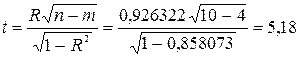
Розрахункое значення t-статистики порівнюється за абсолютною величиною з табличним t10-4 = 1,943. Оскільки розрахункове значення більше, коефіцієнт кореляції є статистично значущим.
4. Побудова прогнозу по регресійній моделі
Точковий прогноз. Задані прогнозні Х01 , Х02 , Х03 для певного 0-го періоду. Прогнозне значення Y0 для цього періоду розраховується по формулі:
Y0 = ![]()
Якщо Х01 = 252, Х02 =0,35, а Х03 = 128 (задаються дослідником або визначаються по продовженню тенденції їх зміни), то точковий прогноз на 0-й період складе:
Y0 = ![]() = -23,83+0,23 * 252 + 9,02 0,35 + 0,10*128 = 49,07704,
= -23,83+0,23 * 252 + 9,02 0,35 + 0,10*128 = 49,07704,
чи в матричному вигляді:
Y = BТ *X0 =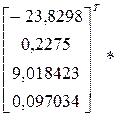
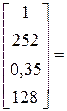 49,07704
49,07704
Де В – матриця оцінок параметрів моделі. Його стандартна похибка складає
![]() 16,60574
16,60574
Інтервальний прогноз визначається як
![]() =49,07704
=49,07704 ![]() 1,943*24,1312*
1,943*24,1312*![]() = =49,07704
= =49,07704 ![]() 11,58627
11,58627