Лабораторная работа: Класична лінійна регресія
Значущість всієї моделі в цілому будемо проводити для рівня значущості a=0,05 за допомогою F-крітерія при (m-1) і (n-m) ступенях свободи. Розрахункове значення F-критерію розраховується по формулі:
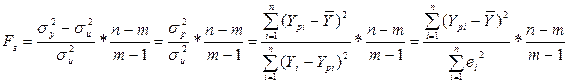
де ![]() ,
, ![]()
Y– спостеріганні значення фактора (вихідні дані),
n – число спостережень,
m – число оцінюваних параметрів.
Нульова гіпотеза для перевірки значущості моделі: Н0 : b0 = b1 = …… = bm = 0.
Проведемо необхідні попередні розрахунки.
Використовуючи вихідну матрицю Х і побудовану модель, отримуємо розрахункові Yp:
Yp = X*BT і залишки е = Y - Yp :
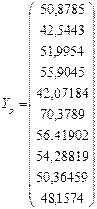
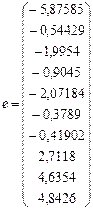
Сума квадратів відхилень значень регресії від середнього та сума залишків дорівнює:
![]() 583,5752
583,5752 ![]() ,
,
![]()
Табличне значення для (m-1), (n-m) F-критерію (0,95) = 4,76. Оскільки Fp >Fтабл , модель можна вважати статистично значимою. (нульова гіпотеза відхиляється).
Далі оцінюєтья значущість кожного з параметрів bj .за допомогою t-статистики.
3. Оцінка значущості окремих коефіцієнтів регресії.
Гіпотезу про значущість кожного з параметрів bj економетрічної моделі можна виконати за допомогою t-крітерію. Нульова гіпотеза, найбільш поширена притестуванні економетричної моделі - bjнесуттєво відрізняються від 0, тобто H0 : bj = 0. Поширеність такої постанови нульової гіпотези – в тому, що якщо вона підтверджується, то це має означати, що відповідний Xj статистично незначущо впливає на Y, його вплив з високою вірогідністю дорівнює 0, залежності між Y та Х практично немає і відповідна змінна повинна бути виключена з моделі. Виключенням є випадок, коли при незначущому bj залежність між X і Y таки існує, але нелінійна. В цьому випадку треба змінити специфікацію моделі (надати їй іншу аналітичну форму).
Розрахункове значення t-критерію:

де Sbj – стандартна помилка коефіцієнта bj ,
cjj – діагональний j-й елемент матриці С=![]()
Визначимо значення стандартних помилок коефіцієнтів регресії Sbj як корінь з дисперсії коефіцієнта bj :
![]()
Для отримання оцінок дисперсії Dj розрахуємо дисперсійно-коваріаційну матрицю (іноді її називають коваріаційною).
Розраховується вона за формулою
![]() ,
,
де ![]() - дисперсія залишків
- дисперсія залишків
Матрицю С=![]() ми маємо.
ми маємо.