Лабораторная работа: Прикладная механика
α1 = 0;
α2 = φ1 = 2,06º;
α0 = φ1 + φ2 = 2,06º + (-0,565º) = 1,495º;
α3 = φ1 + φ2 + φ3 = 1,925º;
α4 = φ1 + φ2 + φ3 + φ4 = 1,085º.
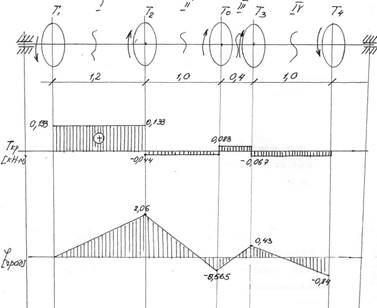
Рис. 2. Вал и его эпюры
Задача 2
Для статически определимого бруса квадратного ступенчато-переменного сечения, нагруженного показанными на рис.3 осевыми сосредоточенными нагрузками, требуется:
1. Построить эпюру продольных сил.
2. Из условия прочности определить площади и размеры сечений участков бруса.
3. Вычислить абсолютные продольные деформации участков бруса и построить эпюру его осевых перемещений.
4. Сделать эскиз ступенчатого бруса.
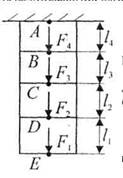
Рис.3. Ступенчатый брус
Дано:
F 1 = +94 kH ; l 1 =2,6 м;
F 2 =-56 kH ; l 2 =2,0 м;
F 3 = +37 кН; l 3 = 1,2 м;
F 4 = +84 кН; l 4 =3,2 м;
[σ ]= 170 МПа;Е = 1,9·105 МПа.
Решение:
1. Изображаем в масштабе (по длине) брус и указываем нагрузку и размеры участков. На каждом участке проводим сечение и рассматриваем равновесие нижней отсеченной части, находим продольную силу в этих сечениях. Так как на исходном рисунке все силы направлены вниз, то продольная сила в любом сечении будет равна алгебраической сумме всех заданных сил, находящихся ниже данного сечения.
Сечение 1-1:
N 1 = F 1 =94 кН;
Сечение 2-2:
N 2 = F 1 + F 2 =90+(-56)= 38 кН;
Сечение 3-3: N 3 = F 1 + F 2 + F 3 = 90 + (-56) + 37 = 75 кН;
Сечение 4-4: N 4 = F 1 + F 2 + F 3 + F 4 = 90 + (-56) + 37 + 84 = 159 кН.
По этим данным строим эпюру N , учитывая, что на протяжении участка продольная сила постоянна.