Отчет по практике: Диференціальні рівняння вищих порядків

Відзначемо, що система рівняння (6) завжди є розв’язком, бо існує розв’язок задачі Коші (4) – (5)

На практиці для диференціального рівняння другого порятку можуть бути задані інші умови замість умов Коші. Ними можуть бути крайові умови: і геометрична задача полягає у знаходженні інтигральної кривої диференціального рівняння (4), яка проходить через дві точки ,.

Примітка. Якщодиференціального рівняння (3) має один розвязок відносно , то воно рівносильне диференційномурівняню , де

Якщо ж диференціальне рівняння (3) має декілька розв’язком відносно , то воно рівносильне сукупності диференціальних рівнянь.

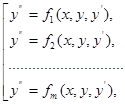де

Зниження порядку диференціальних другого порядку

Основним методом інтегрування (знаходження загального розвязку або загального інтеграла) диференціальних рівнянь вищого порядку є зниження їх порядку і зведення до інтегрування диференціальних рівнянь першого порятку. Розглянемо деякі можливі видатки зниження порядку диференціальних рівнянь другого порядку.

1. Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:

(7).

У цьому випадку робимо заміну і отримуємо диференціальне рівняння першого порядку стосовно невідомої функції Z:

Якщо знайдемо загальний розв’язок , рівнянь (8) то далі інтегруємо рівняння ; якщо ж знайдемо загальний інтеграл то для знаходження розв’язків диференціального рівняння (7) отримуємо наявне диференціальних рівнянь першого порятку

2. Диференціальне рівняння не містить явно аргументах х, тобто має вигляд

(9)

У розв’язаному випадку приймаємо за невідому функцію а й аргументи вважаємо у . Тоді маємо:

Підставимо вирази для у’,y” у рівняння (9), отримаємо відносно функцію диференціальних рівнянь першого порядку:

(10)

Якщо знайдемо загальний розв’язок рівняння (10), то дані інтнгруєм явне диференціальне рівняння першого порядку яке є з розв’язком функції змінними; якщо ж знайдено загальний інтеграл рівняння (17.10), то дані інтегруємо наявне диференційне рівняння першого порядку.

Диференціальне рівняння (3) є однорідним відносно функції у та її похідних і

тобто

У цьому випадку виконуємо заміну де z = z (x). Знаходимо Підготовимо вирази для та у рівняння (3) і використовуємо його однорідність:

У результаті приходимо до диференціальних рівнянь першого порятку стосовно функції

(11)

яке з точністюдо розвязку рівносильне рівняню (3)

Якщо знайдемо загальний розвязок рівняння (11), то речі інтегруємо розв’язане дифененційне рівняння першого порядку , яке є з відокремлюваними змінними; якщо ж знайдемо загальний інтеграл то приходимо до інтегрування наявного диференціального рівняння першого порядку: