Реферат: Аксиоматика векторного пространства

Глава 2

1. Некоторые векторные равенства

Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные соотношения являются, образно выражаясь, ключами к решению широкого класса задач.

I Основное соотношение. Во всяком треугольнике ЛВС выполняется равенство

(I)

Где М – центроид (точка пересечения медиан) треугольника АВС.

Докажем соотношение (I).

П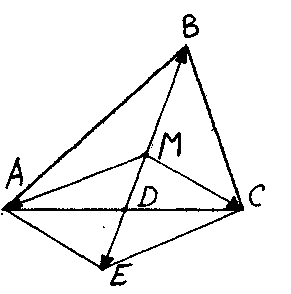усть М – центроид треугольника АВС. Соединим точку М со всеми вершинами треугольника. Прямая МВ пересекает сторону АС треугольника АВС в точке О, являющейся серединой стороны АС. На прямой ВМ откладываем МЕ = ВМ и соединяем точку Е с вершинами А и С. очевидно, что АМСЕ –параллелограмм. Поэтому . Откуда . Так как , то . Ч.т.д.

Задача. Доказать, что если М – центроид треугольника АВС и О -произвольная точка пространства, то выполняется равенство

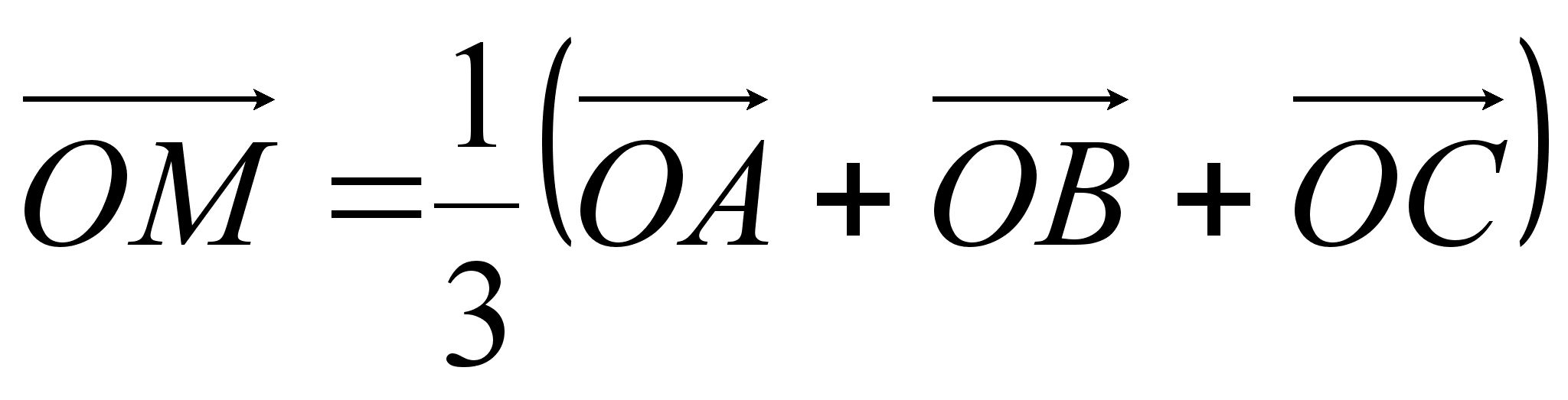(1)

Доказательство:

Запишем следующие векторные равенства:

Сложив эти равенства по частям, получаем:

,

откуда

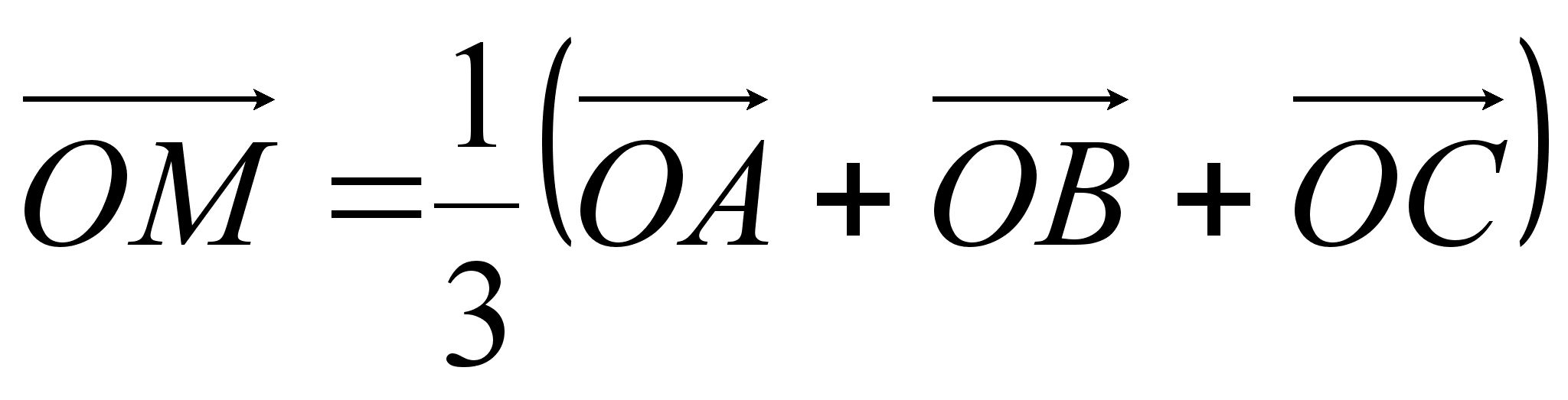
Доказанное равенство также следует отнести к основным векторным соотношениям, так как оно часто используется в решении многих задач.

II Основное соотношения. В треугольнике АВС на стороне АС взята точка D так, что АD : DС = m : n.

Тогда имеет месть следующее соотношение:

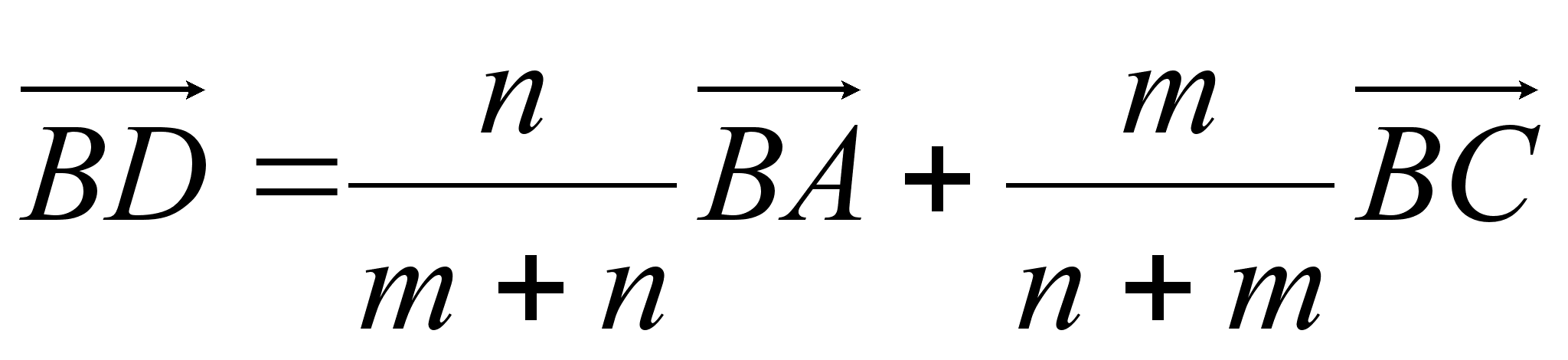(II)

Доказательство:

Из треугольника АВС имеем:

.

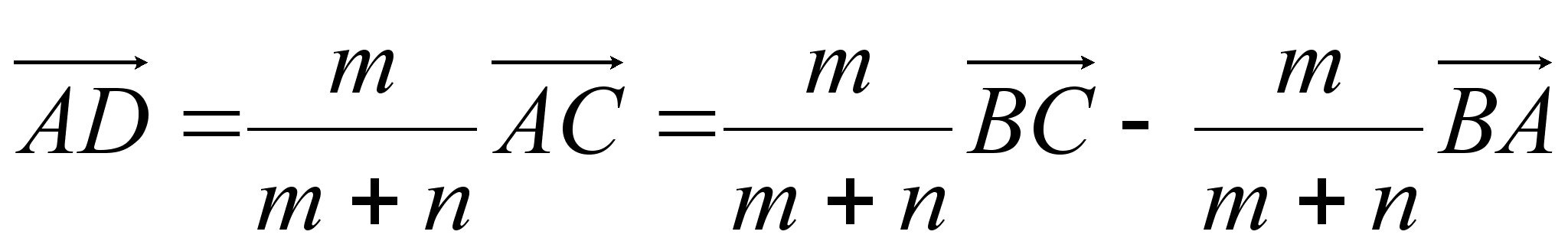
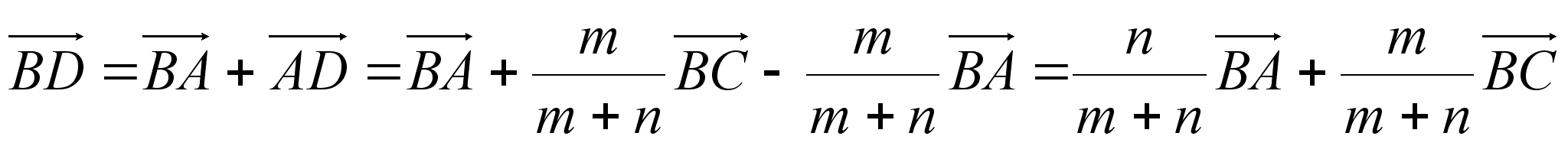Ч.т.д.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--