Реферат: Аксиоматика векторного пространства

,

но, , т.к. . Следовательно

.

длины векторов и найдем по теореме Пифагора.

Таким образом

Тогда

Ответ: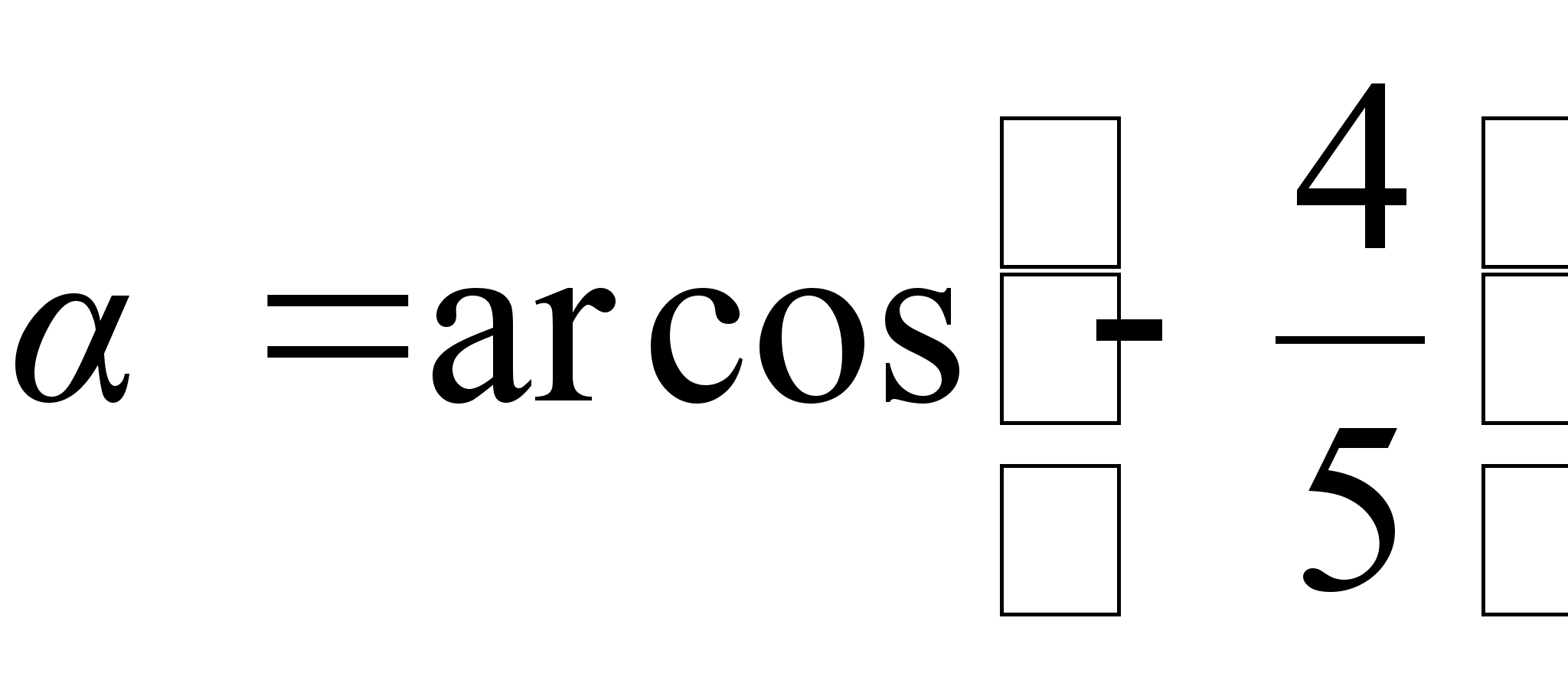

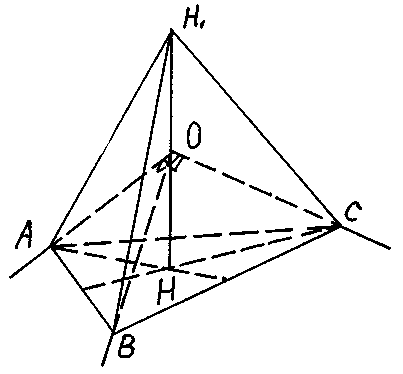
Задача. На ребрах прямоугольного трехгранного угла с вершиной О отложены равные отрезки ОА, ОВ, ОС. Из точки О на плоскости ABC опущен перпендикуляр ОН. Доказать, что если точка Н₁ симметрична точке Н относительно вершины О, то тетраэдр Н₁ ABC правильный.

Решение:

Примем вершину О трехгранного угла за начало векторов. Тогда

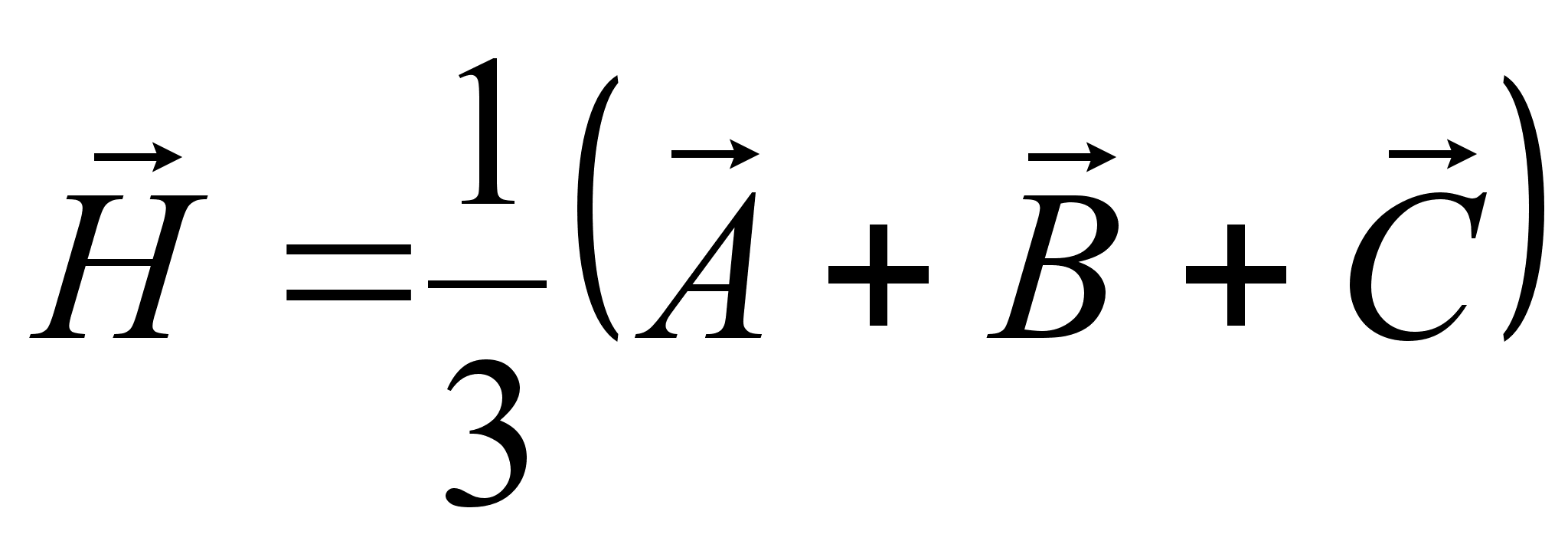
и .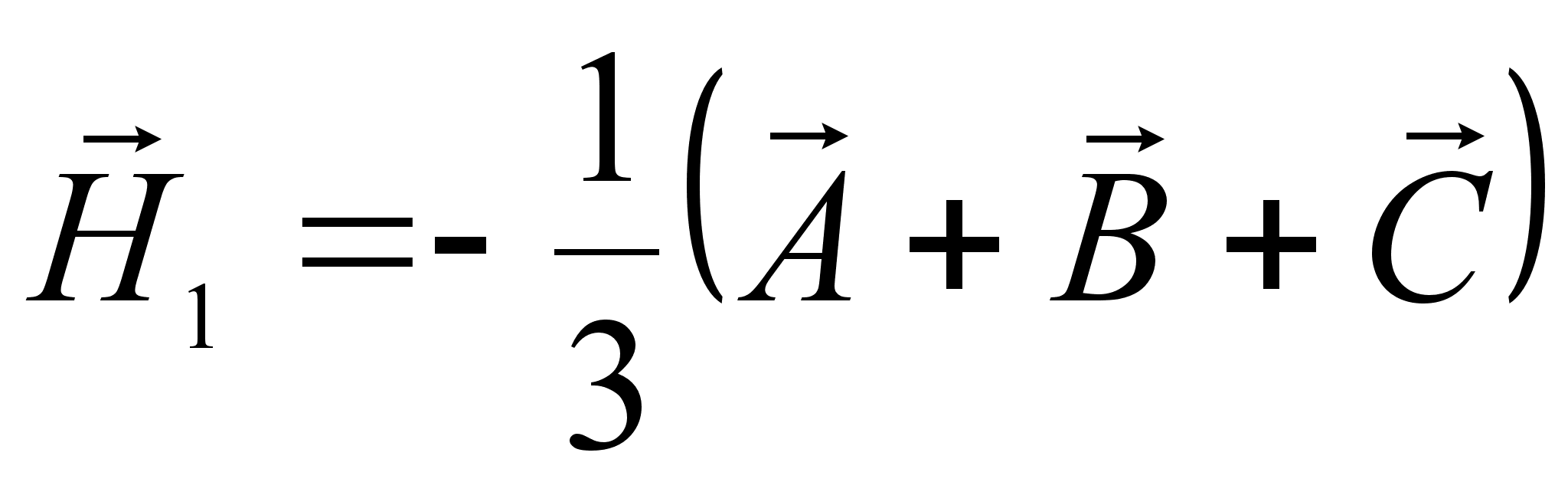

Следовательно,

,

.

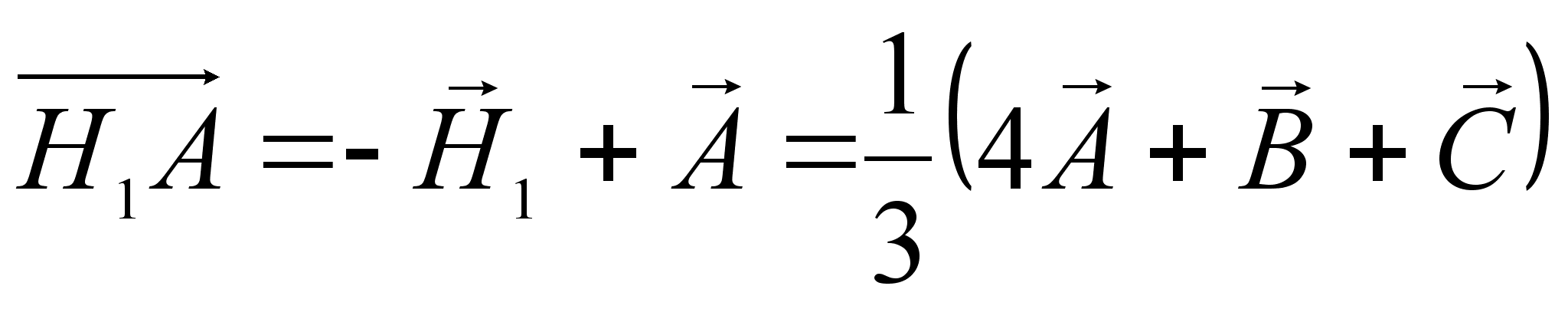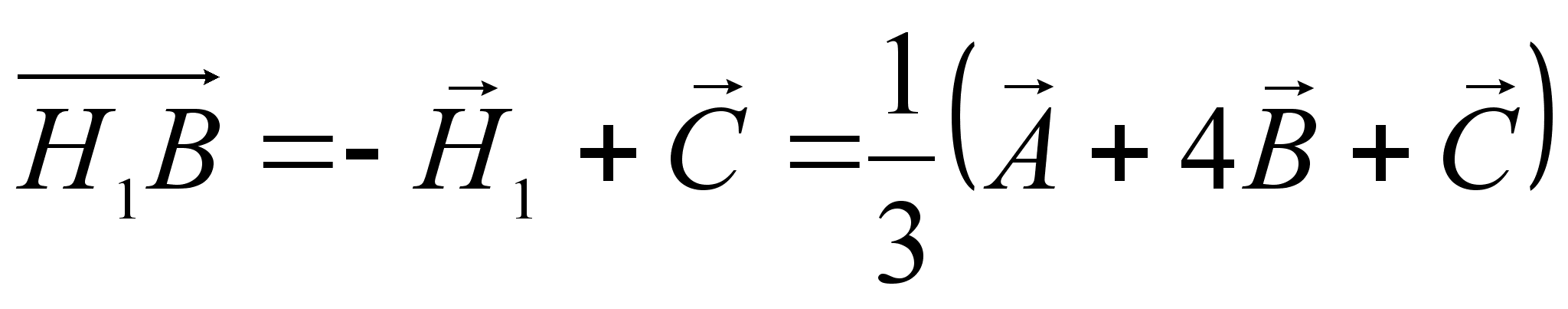Найдем

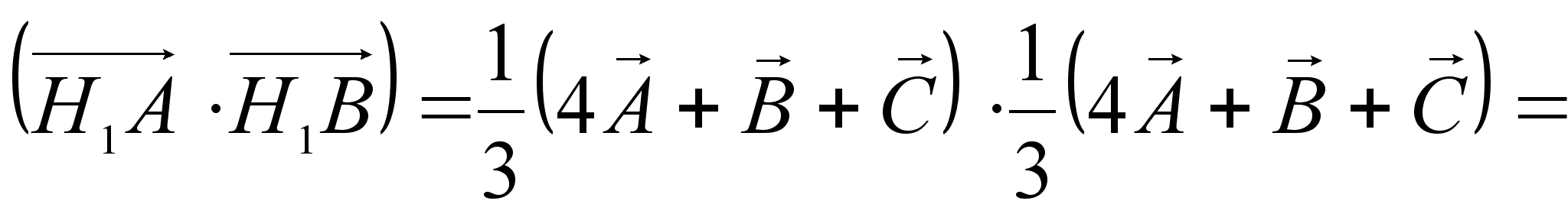
Учитывая, что и , имеем: .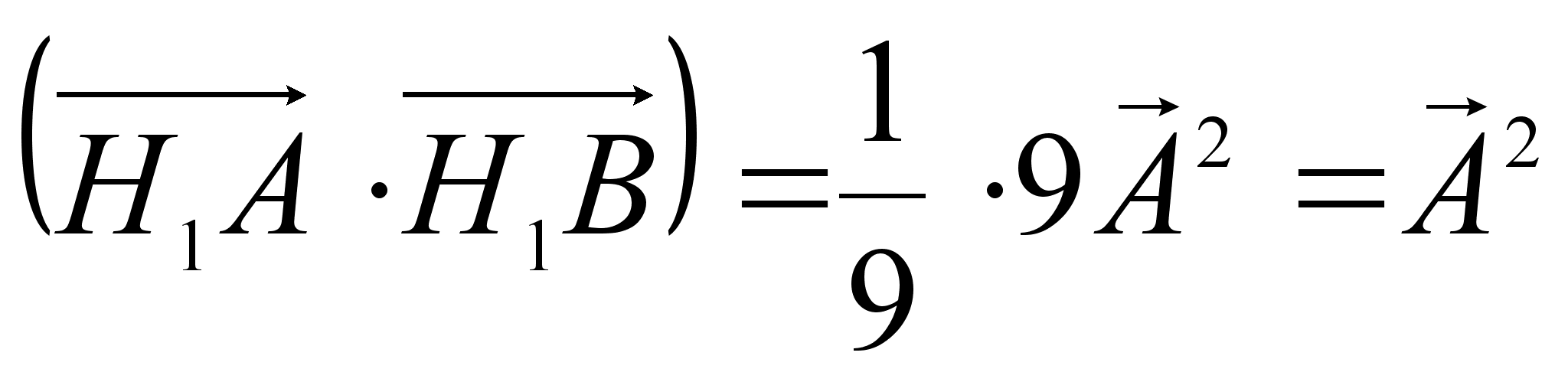

Далее находим:

,

,

.

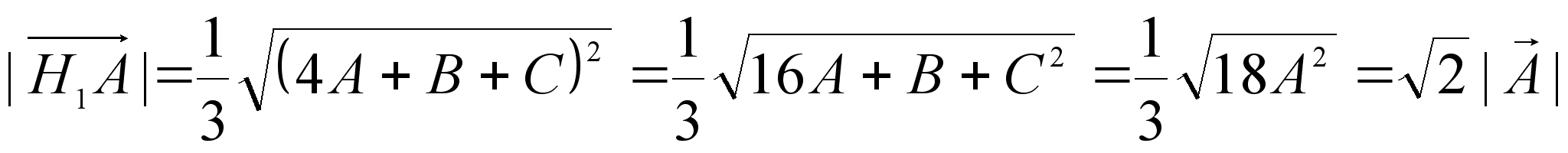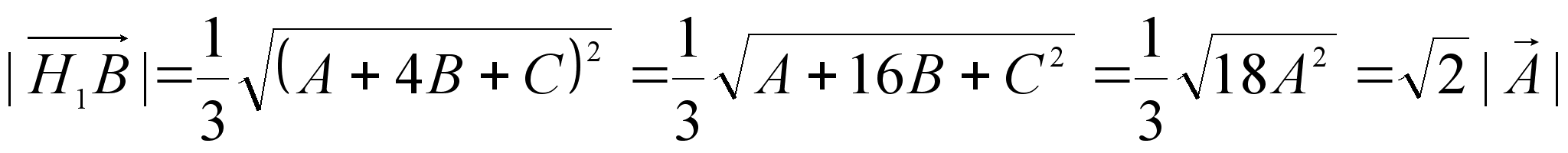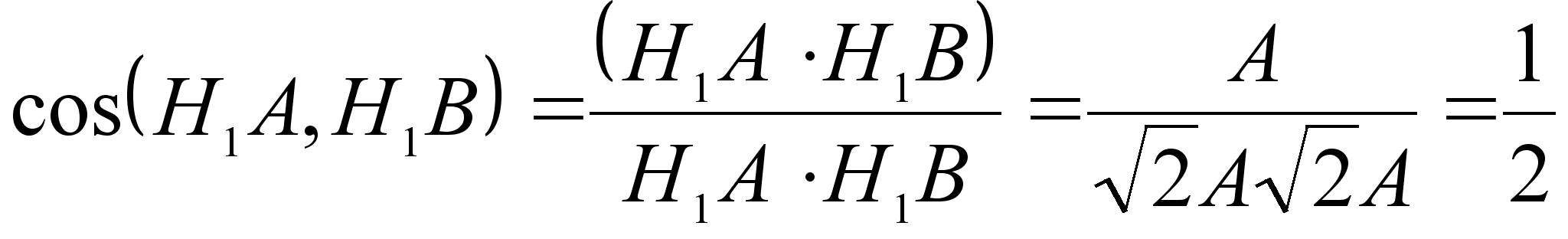Это значит , что отрезки H₁A и H₁B равны и образуют угол 60°, т.е. треугольник H₁AB правильный.

Аналогично устанавливается, что две другие грани H₁BC и H₁CA являются равносторонними треугольниками и вследствие этого тетраэдр правильный.

Задача. Доказать, что можно построить треугольник, стороны которого равны и параллельна медианам данного треугольника ABC.

Решение.

О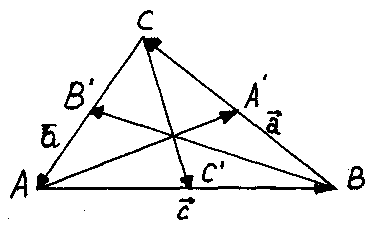бозначим середины сторон ВС, СА и АВ соответственно А’, B’, C’. Выразим векторы, представляющие медианы треугольника ABC, через , , (через стороны данного треугольника):