Реферат: Аксиоматика векторного пространства

,

.

Составим сумму сторон треугольника ABC

.

Но так как векторы и образуют данный треугольник ABC, то их сумма равна нулю, следовательно, и . А это значит, что из векторов можно построить треугольник.

З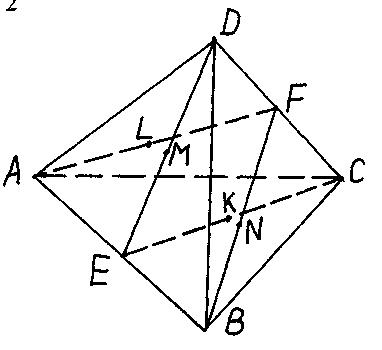адача. В треугольнике ABCD точка Е и F – середина рёбер АВ и CD соответственно. Доказать, что середины отрезков СЕ, DE, AF и BF являются вершинами параллелограмма.

Решение. Пусть К, L, М, N - середины отрезков СЕ, DE, AF и BF, соответственно. Доказать, что середины отрезков СЕ, DE, AF и BF являются вершинами параллелограмма.

Докажем равенство векторов и , выразив их через векторы , , , , где О – произвольная точка.

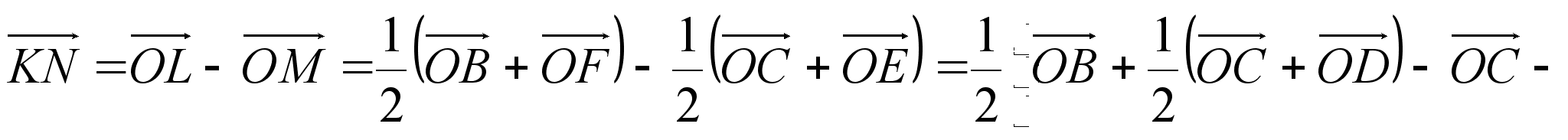
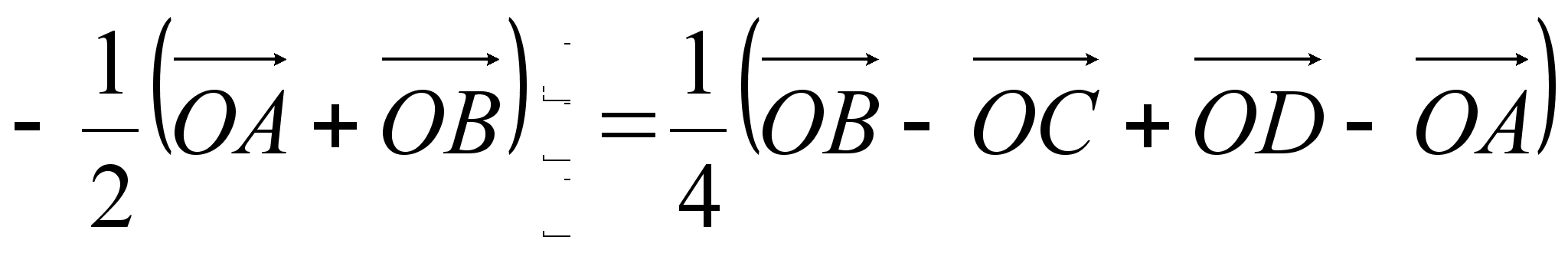(1)

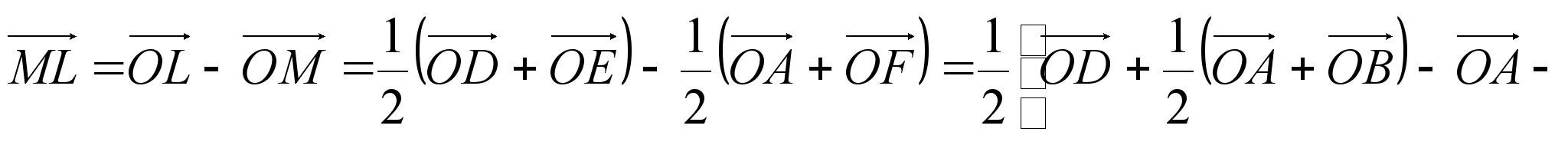
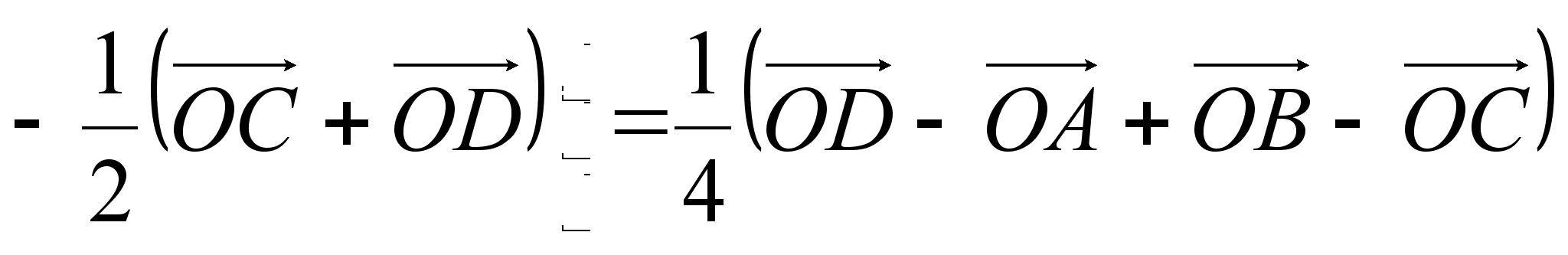. (2)

Ч. Т. Д.

Задача. Точки К, L, M на сторонах АС, ВС, АВ треугольника ABC таковы, что 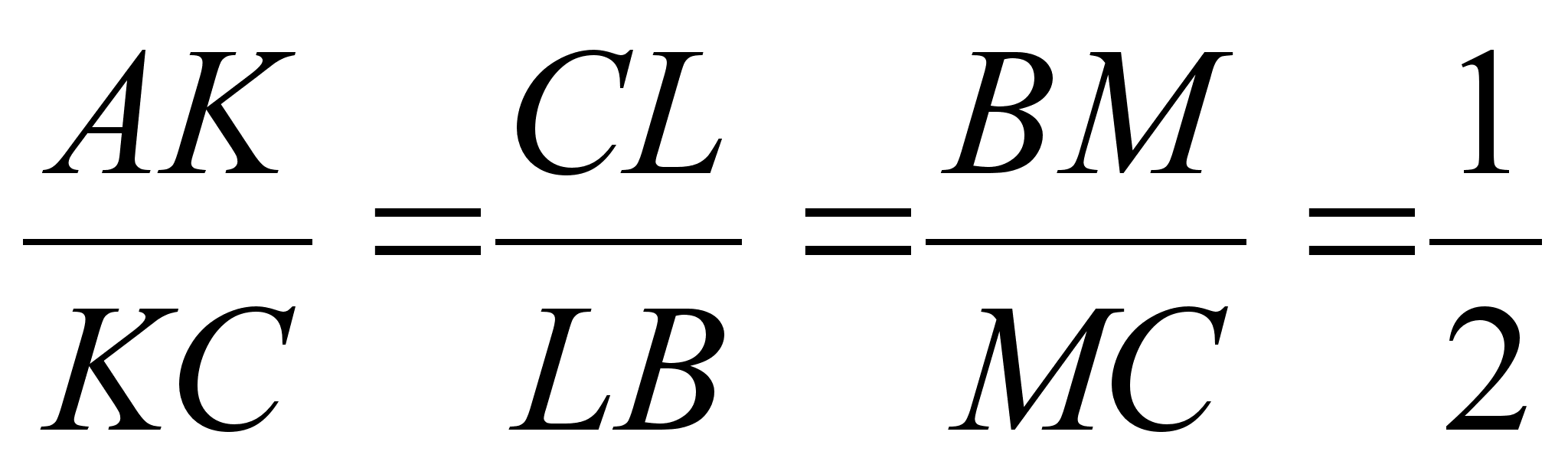, N – середина сторона АС. Найти отношение в котором точка пересечения отрезков KL и MN делит отрезок KL.

Решение.

Обозначим через О точку пересечения отрезков MN и KL и через х отношение KO : KL. Тогда . Учитывая, что L – середина МС и , получаем

Так как точка О лежит на прямой MN, то . Откуда . Значит, .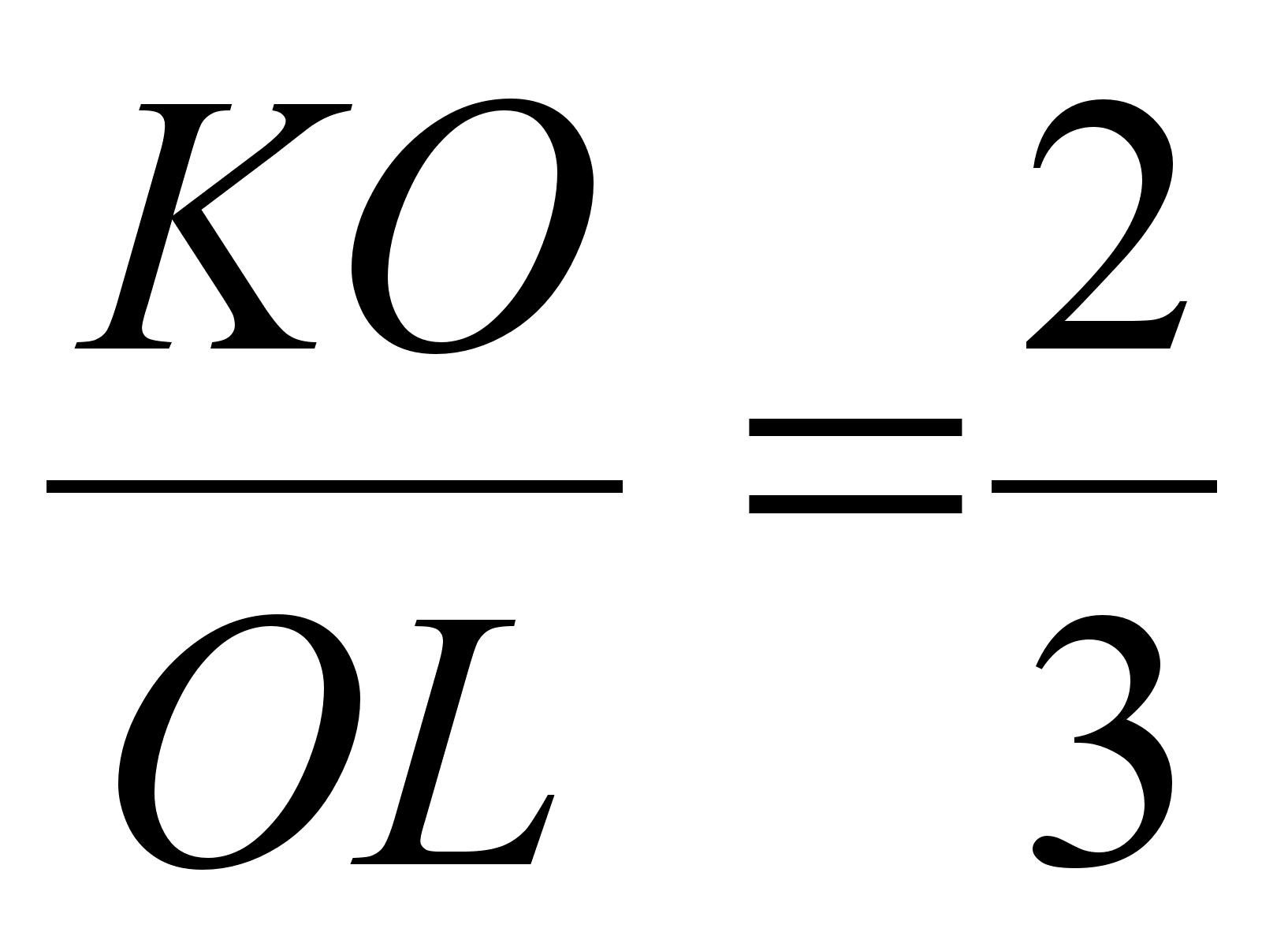

Ответ: KO : OL = 2:3

З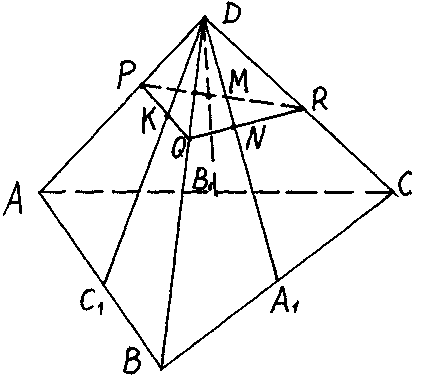адача. Отрезки DA₁, DB₁, DC₁ – медианы граней BCD, ACD и ABD тетраэдра ABCD соответственно. Точки К, М, N делят отрезки DA₁, DB₁, DC₁ в отношении 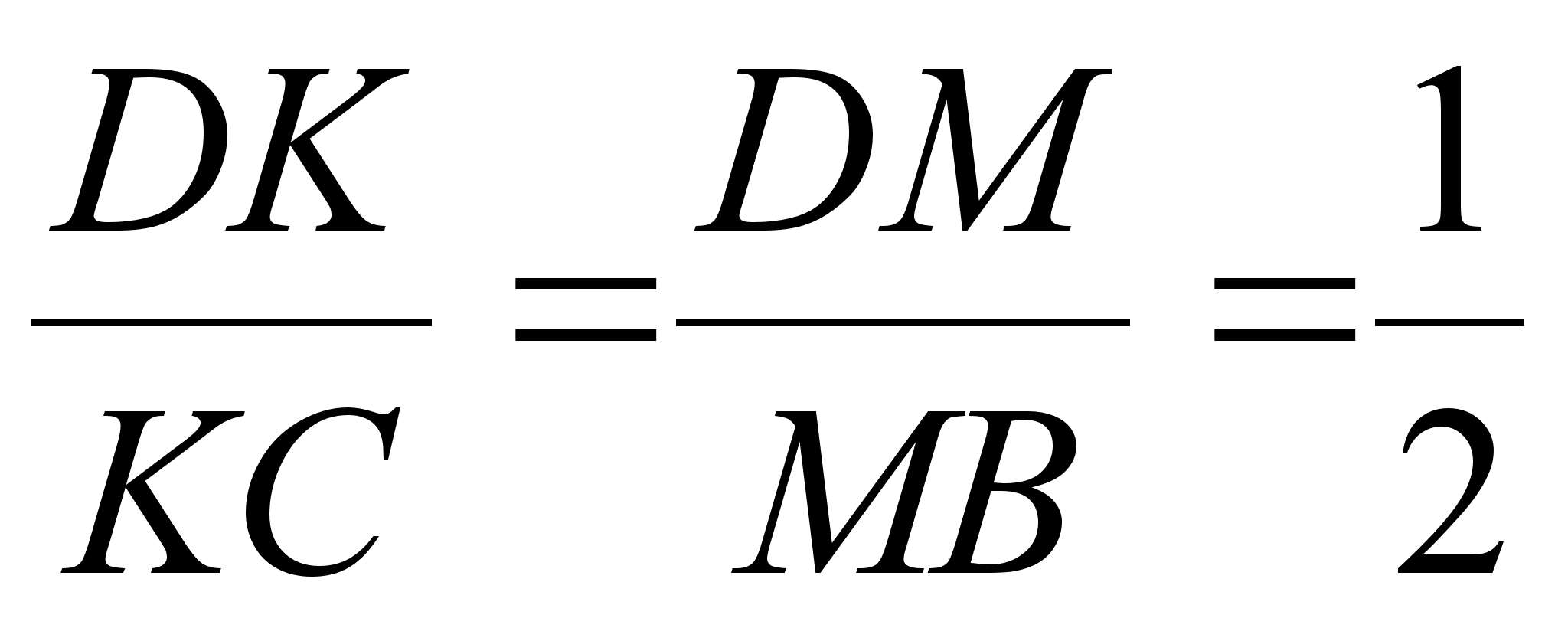, 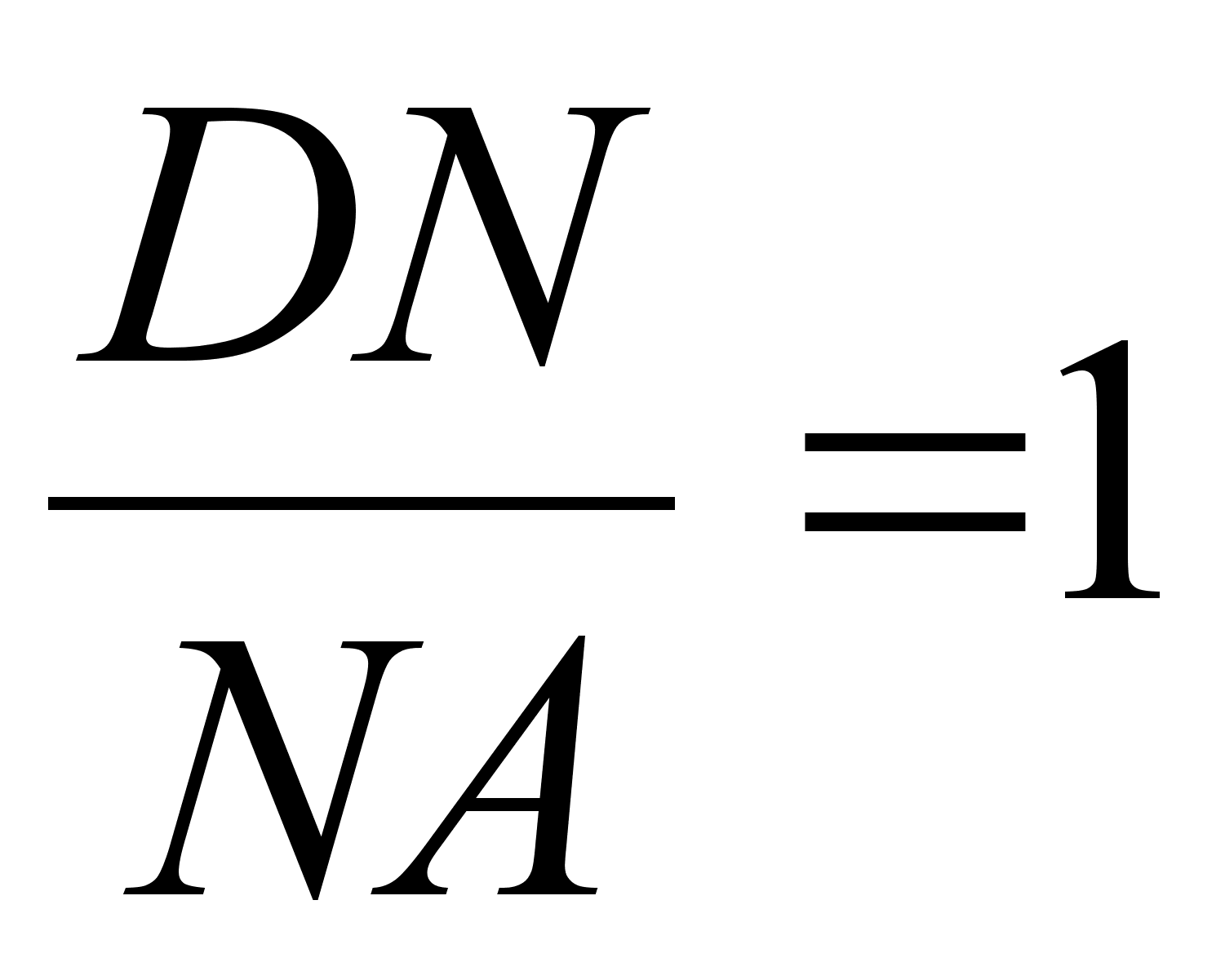. В каком отношении плоскость KMN делит ребра DA и DB ?

Решение.

Пусть плоскость KMN пересекает ребра DA, DB и DC тетраэдра ABCD в точках Р, Q, R соответственно.

Точки А₁, В₁, С₁ – середины отрезков ВС, АС, АВ соответственно. Следовательно,

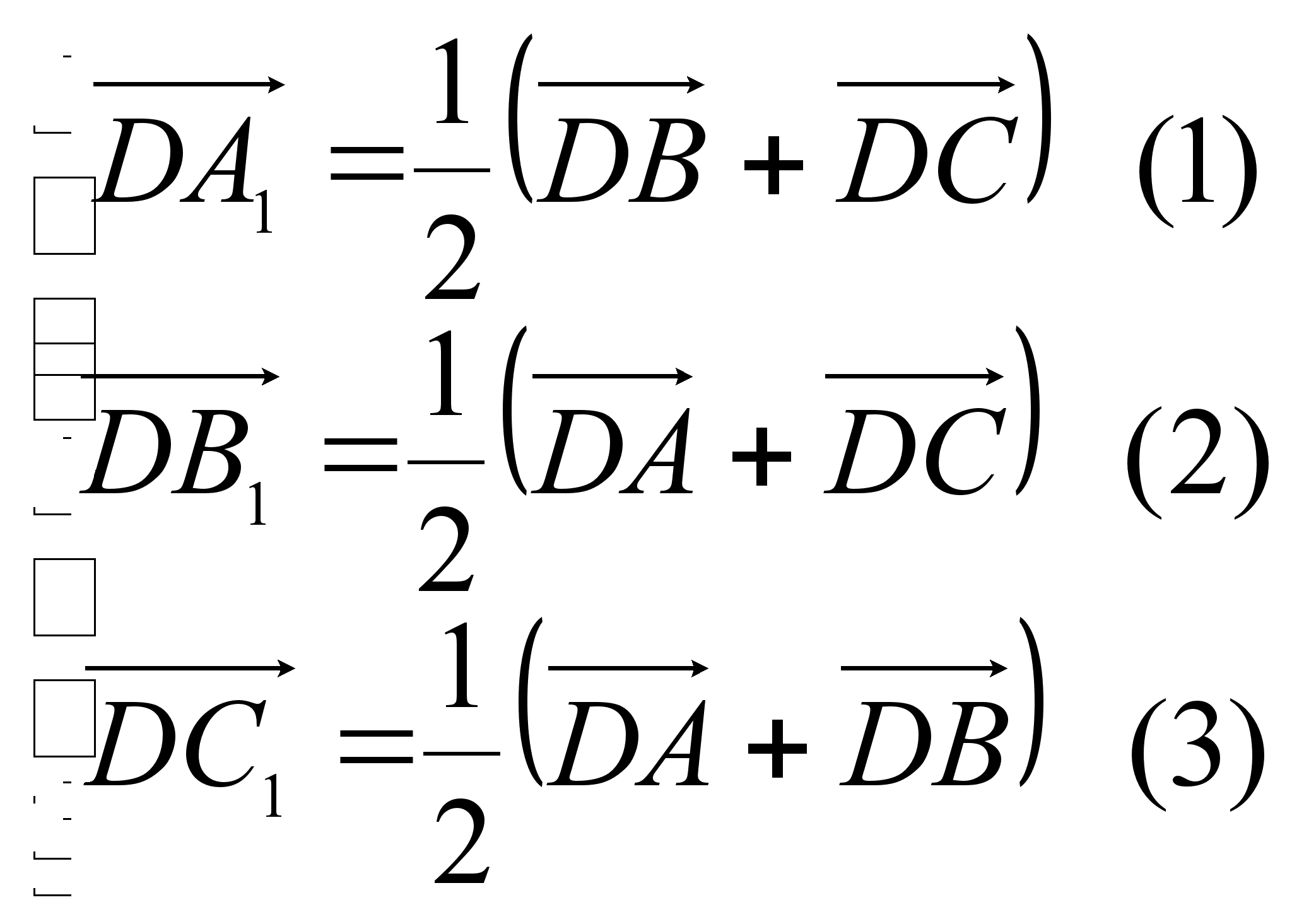
Решив эту систему, (например, сложив (1) и (2), и вычтя (3) получим

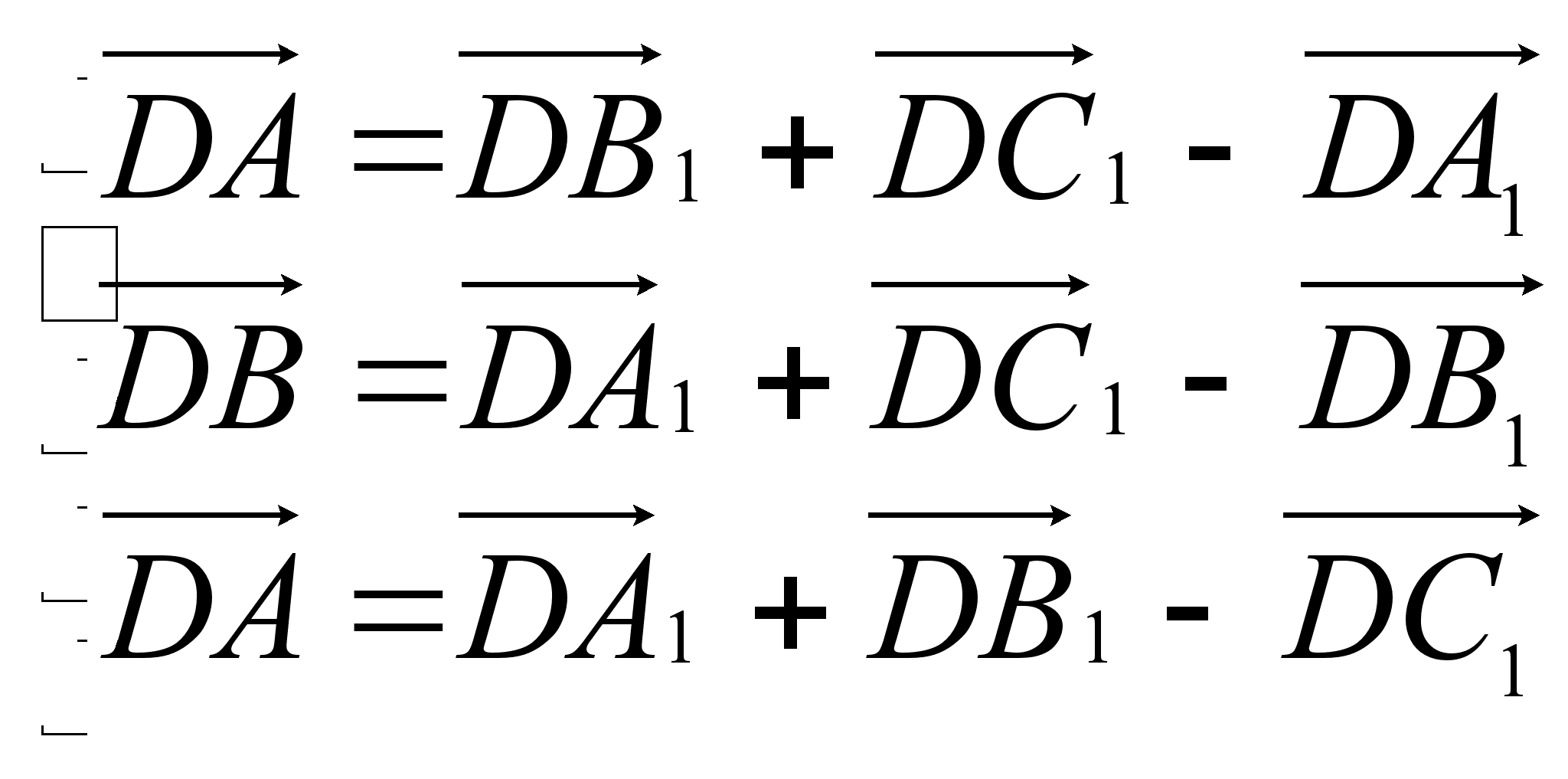
Пусть . Тогда, учитывая , , ,

имеем

, и, т.к. точки К, М, N, Р лежат в одной плоскости, то

.