Реферат: Атомические разложения функций в пространстве Харди
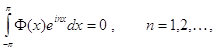
а тогда
.
Пусть 
. Для построения искомой функции 
положим
, 
, 
.
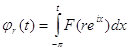Функции 
, , имеют равномерно ограниченную по r вариацию на 
:
.
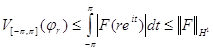Следовательно, по теореме Хелли [2] найдутся функция ограниченной вариации 
и последовательность 
, такие, что 
в каждой точке и
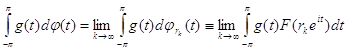(32)
для любой функции 
. При этом для n=1,2,...
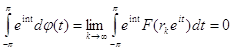
(мы учли аналитичность функции F(z) в единичном круге) и , следовательно, по теореме 3 абсолютно непрерывна : существует функция , для которой
,
Тогда
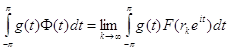, (33)
Зафиксируем число 
. Функция 
, аналитична в круге 
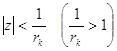, поэтому согласно утверждению 1
, 
.
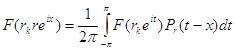В пределе при 
из последнего равенства вытекает, что
, 
, .
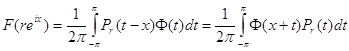Равенство 1) , а вместе с ним и теорема 4 доказаны.
§I.3.Пространства 
и 
.
Обозначим через 
класс тех функций 
, , которые являются граничными значениями функций из 
, т.е. представимы в виде
для п.в. , 
.
В силу пунктов 3) и 2) теоремы 4