Реферат: Атомические разложения функций в пространстве Харди

Пусть , где - конечная или бесконечная последовательность дополнительных интервалов множества F, и для

.

Очевидно, что - открытое множество и .

Рассмотрим для данных функцию , построенную в лемме 1 для числа e и множества . Тогда нетрудно проверить[3], что если , а , то разность

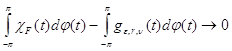. (23)

Но в силу (19) и равномерной сходимости ряда (21) (так как ряд Фурье бесконечно дифференцируемой функции сходится равномерно)

,

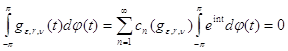и мы получаем равенство (20).

Перейдем к доказательству леммы 1. Нам понадобится

ОпределениеI.4.

Средние Фейера - это средние вида

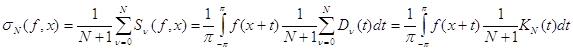
, где , , - ядро Дирихле,

, - ядро Фейера.

Отметим, что при ядро Фейера обладает следующими свойствами: а) , ; б) ,

Мз которых вытекает, что для и

,

Также известно [3], что средние Фейера равномерно сходятся к .

Пусть f(t) - непрерывная на [-p, p] функция, для которой

и

Так как средние Фейера равномерно сходятся к и

, то существует тригонометрический полином

(24)

такой, что

(25)

Пусть . Рассмотрим для каждого d>0 такую функцию , что

,

(функцию можно построить следующим образом: взять замкнутое множество с мерой , достаточно близкой к 2p, и положить

).