Реферат: Атомические разложения функций в пространстве Харди

.

Тогда для

.

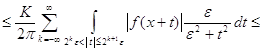
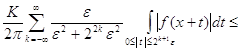
Неравенство (13) доказано. Возьмем слабый тип (1,1) оператора . Используя его, найдем такую последовательность функций ,что

,

( 14 )

для п.в. .

Согласно (13) при xÎ (-p,p)

Учитывая , что по теореме 1 для каждого xÎ [-p, p] и (14)

из последней оценки получим

при r®1.

Теорема 2 доказана.

Замечание1.

Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p, p] , когда точка re^it стремится к e^ix по некасательному к окружности пути.

§I.2.Пространства H^p .

Определение I.3.

Пространство - совокупность аналитических в единичном круге функций F (z) , для которых конечна норма

. (15)

Пусть комплекснозначная функция удовлетворяет условиям

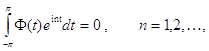(16)

тогда функция F (z) , определенная равенством

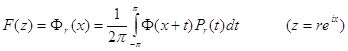(17)

принадлежит пространству , причем

. (18)