Реферат: Динамический синтез системы управления

Из табл. 1.4 видно, что все коэффициенты характеристического уравнения (1.14) положительны, что является необходимым условием устойчивости системы.

Согласно алгебраическому критерию Льенара-Шипара для устойчивости системы необходимо и достаточно, чтобы при положительных коэффициентах характеристического уравнения при четном n , все определители Гурвица нечетных порядков были больше нуля.

В нашем случае n =4. Вычислим определители матрицы Гурвица третьего и первого порядков:

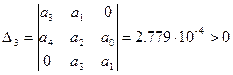, (1.16)

. (1.17)

Определители матриц Гурвица первого и третьего порядков больше нуля, следовательно, нескорректированная замкнутая САР является устойчивой.

Проверим устойчивость системы по логарифмическим амплитудной и фазовой характеристикам (ЛАХ и ЛФХ) разомкнутого контура САР с применением частотного критерия устойчивости Найквиста.

ЛАХ и ЛФХ разомкнутой системы строятся согласно следующим формулам:

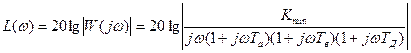, (1.18)

. (1.19)

Для построения располагаемой асимптотической логарифмической амплитудной характеристики найдём вспомогательные данные - частоты сопряжения и значение 20lgK:

,

,

,

Зная ЛАХ для каждого типового звена, являющегося сомножителем передаточной функции (1.12), можно найти асимптотическую ЛАХ системы, как сумму ЛАХ типовых звеньев.

ЛАХ и ЛФХ для разомкнутой нескорректированной САР с пропорциональным регулятором с передаточной функцией (1.12) изображены на рисунке 1.3.

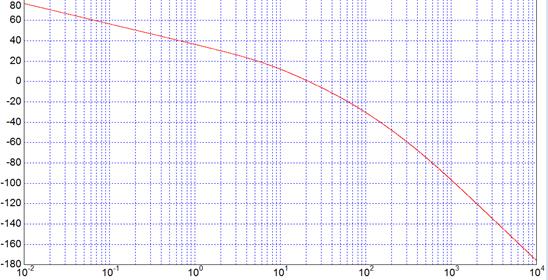
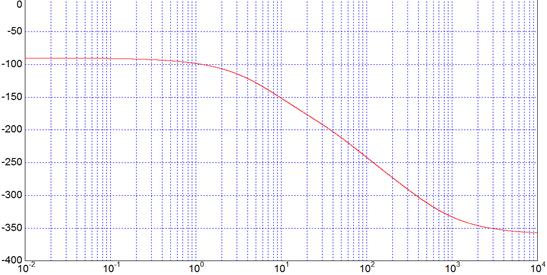
Рисунок 1.3 - ЛАХ и ЛФХ для разомкнутой нескорректированной САР с пропорциональным регулятором

По ЛЧХ разомкнутой системы можно оценить устойчивость замкнутой системы по критерию Найквиста. Устойчивая в разомкнутом состоянии система будет устойчива в замкнутом состоянии, если выполняется равенство: , где - число положительных переходов ФЧХ через один из критических уровней в диапазоне положительности ЛАХ; - число отрицательных переходов; - число правых полюсов.

Согласно (1.12) разомкнутая система не имеет правых корней. Из рисунка 1.3 видно, что количество отрицательных переходов , количество положительных переходов. Так как , то . Следовательно, замкнутая система устойчива.

По графикам ЛАХ и ЛФХ (рисунок 1.3) определим частоту среза и критическую частоту.

Частота среза разомкнутой системы, найденная по графику ЛАХ (пересечение ЛАХ уровня 0дБ), равна:

Критическая частота находится по графику ЛФХ (пересечение ЛФХ уровня -180):

По графикам ЛАХ и ЛФХ разомкнутой системы также можно определить запасы устойчивости системы по модулю и по фазе. На рисунке 1.3 отмечены запасы устойчивости по амплитуде и фазе:

дБ; (1.20)

. (1.21)

1.4 Исследование замкнутой САР

График переходной функция h(t) (по выходу ДОС) для замкнутой системы, полученный методом компьютерного моделирования в среде Vissim приведен на рисунке 1.4.

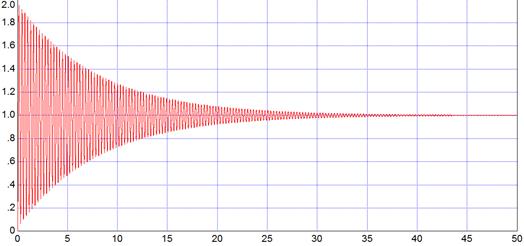
Рисунок 1.4 - Переходная функция h(t) для замкнутой САР

Как видно из графика переходной функции h(t) , , следовательно, система устойчива.

Определим прямые показатели качества переходного процесса.

а) Перерегулирование определяется согласно формуле:

. (1.22)

б) Время регулирования — время, за которое график переходного процесса укладывается в 5% «коридор» от установившегося значения.

По графику найдем .