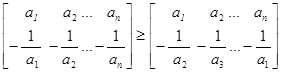Реферат: Доказательства неравенств с помощью одномонотонных последовательностей

Складывая эти неравенства, мы получаем

.

Отделим дроби с одинаковым знаменателем в правой части

.

Вычислив, получаем

.

А это значит, что

Что и требовалось доказать

2.4 Случай с двумя последовательностями из n переменных

Рассмотрим одномонотонные последовательность (а₁ , а₂ , …а_n ) и (b ₁ , b₂ ,…b_n )

Если =a₁ b₁ , и =а₁ b₁ +а₂ b₂ , то 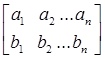=а₁ b₁ +а₂ b₂ …a_n b_n

Теорема 3. Пусть ( а₁ а₂ … а_n ), ( b₁ b_{2 …} b_n ) – одномонотонные последовательности и ()перестановка чисел b₁ b_{2 …} b_n . Тогда

.

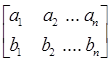
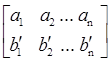Доказательство.

Действительно, если последовательность () отличается от (b₁ b_{2 …} b_n ) то найдется пара чисел k, l (1k<ln) такая, что последовательности (a_k , a_l ) и (b_k , b_l ) не одномонотонны. Значит, поменяв местами числа и и , мы увеличим всю сумму, а значит и всю сумму 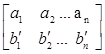. То есть

,

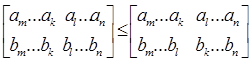так как .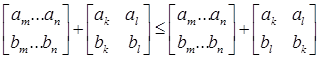

Очевидно, что за конечное число попарных перестановок элементов 2-ой строки можно получить одномонотонную последовательность.

Теорема доказана.

Следствие.

Для любого nN верно

.

Доказательство.

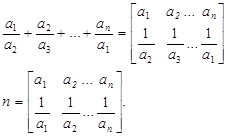
Но последовательности (а₁ а₂ … а_n ) и () не являются одномонотонными, и поэтому мы не можем воспользоваться теоремой 3.

Однако эти последовательности противомонотонны: числа в последовательностях расположены в обратном порядке – самому большому по величине соответствует самое маленькое, а самому маленькому соответствует самое большое. А из противомонотонных последовательностей сделать одномонотонные очень просто – достаточно все числа второй линии взять со знаком минус. В данном случае одномонотонными являются последовательности

(а₁ а₂ … а_n ) и ()

Поэтому