Реферат: Доказательства неравенств с помощью одномонотонных последовательностей

Если =a₁ b₁ , и =а₁ b₁ +а₂ b₂ , и 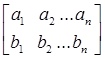=а₁ b₁ +а₂ b₂ …a_n b_n ,

то = а₁ b₁ …d₁ +а₂ b₂ …d₂ + …+a_n b_n …d_n

Теорема 4. Рассмотрим одномонотонные последовательности (а₁ , а₂ , …а_n ), (b ₁ , b₂ ,…b_n ), …, (d₁ , d₂ ,…,d_n ). Тогда

.

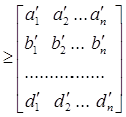Доказательство.

Действительно, если последовательность (a₁ , а₂ , …а_n ), (b'₁ , b'₂ ,…b'_n ), …, (d'₁ , d'₂ ,…,d'_n ) отличается от (а₁ , а₂ , …а_n ), (b ₁ , b₂ ,…b_n ), …, (d₁ , d₂ ,…,d_n ), то найдутся переменные k, l (1k<ln) такие, что последовательности (a_k , a_l ) и (b_k , b_l ) …(d_k , d_l ) не одномонотонны. Значит, поменяв местами числа ,, a_k , a_l … d_k , d_l мы увеличим всю сумму, а значит и всю сумму 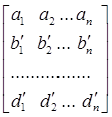. То

есть

,

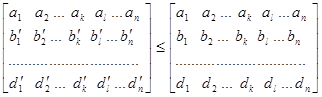так как .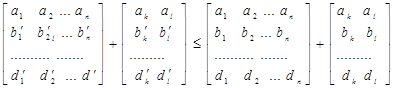

Очевидно, что за конечное число попарных перестановок элементов n-ой строки можно получить одномонотонную последовательность.

Теорема доказана.

Пример

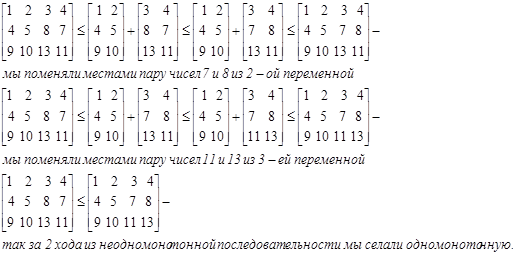
Упражнение 1

Пусть а₁ , а₂ , …а_n - положительные вещественные числа.

Докажите, что

Это неравенство называется неравенством Коши о среднем арифметическом и среднем геометрическом. Докажем его двумя способами

Доказательство.

Перепишем его в виде:

, введя новые переменные

Имеем

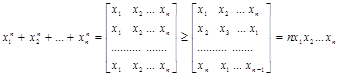
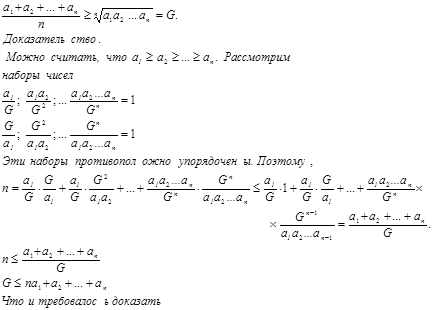
Если сравнить эти два доказательства неравенства, можно заметить, что доказательство с помощью одномонотонных последовательностей гораздо легче в сравнении с доказательством Коши.

неравенство одномонотонный последовательность коши

Заключение

Работая по данной теме, я узнала новый способ доказательства неравенств, вспомнила уже изученные способы доказательства неравенств. Все упражнения в работе я решала сама.

Список использованной литературы