Реферат: Доказательства неравенств с помощью одномонотонных последовательностей

Следствие

Для любого nN верно

(Неравенство Чебышева).

Доказательство.

В силу теоремы 3 справедливы следующие nнеравенства

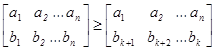
Значит

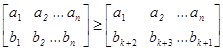
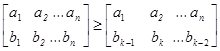
В этих неравенствах левая часть не изменяется, а в правой части элементы второй строки меняются циклически.

Складываем все и получаем

Что и требовалось доказать

Упражнение №1.

Пусть a и b и c – положительные вещественныечисла.

Докажите неравенство.

a³ +b³ +c³ +d³ a² b+b² c+c² d+d² a.

Доказательство.

Заметим, прежде всего, что

a³ +b³ +c³ +d³ =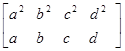, a² b+b² c+c² d+d² a=.

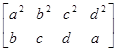А так как последовательности

(a² , b² , c² , d³ ), (a, b , c, d)

одномонотонны, то

.

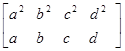
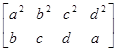А это значит, что a³ +b³ +c³ +d³ a² b+b² c+c² d+d² a.

Что и требовалось доказать.

Доказательство этого неравенства с помощью одномонотонных последовательностей я не могу сравнить с другим доказательством, так как доказать другим способом это неравенство я не смогла.

2.5 Случай с n последовательностями из n переменных